Probabilité - événements indépendants

Conseils

Probabilité - événements indépendants

Dans ce cours, destiné aux élèves de Première spécialité mathématiques, nous allons découvrir la notion d'événements indépendants en probabilité.

Intuitivement deux événements sont indépendants lorsque l'un n'influe pas sur l'autre.

Nous verrons que cette notion peut s'exprimer de deux manières : P(A ∩ B) = P(A) × P(B), ou encore P_A(B) = P(B).

Ce cours est accompagné de nombreux exercices corrigés en vidéo pour vous entraîner, visualiser les situations et maîtriser l'utilisation des arbres de probabilité ou des tableaux pour les événements indépendants.

Exercice type

sur les événements indépendants

Cours

Événements indépendants

• Intuitivement

• 3 façons de dire que A et B sont indépendants

• 3 façons de démontrer que A et B sont indépendants

On démontre que $\rm P_{B}(A)=P(A)$

On calcule séparément $\rm P_{B}(A)$ et $\rm P(A)$ puis on montre qu'ils sont égaux

S'ils ne sont pas égaux, cela signifie que A et B ne pas indépendants, donc A et B sont dépendants.
On démontre que $\rm P_{A}(B)=P(B)$

On calcule séparément $\rm P_{A}(B)$ et $\rm P(B)$ puis on montre qu'ils sont égaux

S'ils ne sont pas égaux, cela signifie que A et B ne pas indépendants, donc A et B sont dépendants.
On démontre que $\rm P(A\cap B)= P(A)\times P(B)$

On calcule séparément $\rm P(A\cap B)$ et $\rm P(A)\times P(B)$ puis on montre qu'ils sont égaux

S'ils ne sont pas égaux, cela signifie que A et B ne pas indépendants, donc A et B sont dépendants.

• Propriétés

• indépendant et incompatible

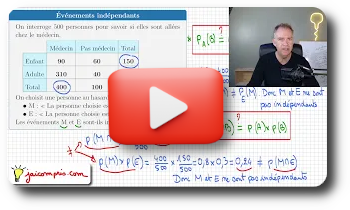
Résumé du cours en vidéo

Exercice 1: évènement indépendants • Première spécialité mathématiques S - ES - STI

On interroge 500 personnes pour savoir si elles sont allées chez le médecin.

	Médecin	Pas médecin	Total
Enfant	$90$	$60$	$150$
Adulte	$310$	$40$	$350$
Total	$400$	$100$	$500$

On choisit une personne au hasard. On note les événements :

$\bullet$ M: « La personne choisie est allée chez le médecin »
$\bullet$ E: « La personne choisie est un enfant »

Les événements M et E sont-ils indépendants?

Exercice 2: évènement indépendants • Première spécialité mathématiques S - ES - STI

Le tableau suivant donne la répartition de 150 élèves en fonction de la langue choisie et de l'activité sportive choisie.

	Tennis	Équitation	Voile
Anglais	$45$	$18$	$ 27$
Allemand	$33$	$9$	$18$

On choisit un élève au hasard.

Les événements « étudier l'allemand » et « pratiquer le tennis » sont-ils indépendants ?
Les événements « étudier l'anglais » et « pratiquer la voile » sont-ils indépendants ?

Exercice 3: succession d'épreuves d'événements indépendants • Première spécialité mathématiques S - ES - STI

On lance deux dés cubiques bien équilibrés avec les faces numérotées de $1$ à $6$. Quelle est la probabilité de faire un double six ?
On lance trois fois de suite une pièce de monnaie. Quelle est la probabilité de ne faire que des "face" ?
On lance la pièce de monnaie puis le dé. Quelle est la probabilité de faire "pile" et un nombre supérieur ou égal à $3$ ?

Exercice 4: succession d'épreuves d'événements indépendants • Première spécialité mathématiques S - ES - STI

Sur son trajet habituel domicile-travail, une automobiliste rencontre deux feux tricolores qui fonctionnent de manière indépendante :

la probabilité de devoir s'arrêter au premier feu est de $\dfrac{1}{3}$.
la probabilité de devoir s'arrêter au second feu est de $\dfrac{5}{12}$.

Quelle est la probabilité que l'automobiliste s'arrête deux fois ?
Quelle est la probabilité que l'automobiliste ne s'arrête à aucun feu sur son trajet ?
Quelle est la probabilité que l'automobiliste s'arrête au moins une fois sur son trajet ?

Exercice 5: succession d'épreuves d'événements indépendants - Première spécialité maths S - ES - STI

Un vendeur a deux rendez-vous dans sa matinée avec des clients. Il va faire signer un contrat à son premier client avec une probabilité de $0,7$ et avec le deuxième client avec une probabilité de $0,4$ (les deux événements sont considérés indépendants).

Quelle est la probabilité de l'événement : "le vendeur ne fait signer aucun contrat" ?
Quelle est la probabilité de l'événement : "le vendeur fait signer au moins un contrat" ?

Exercice 6: Probabilités conditionnelles - Événements indépendants - Première spécialité maths S - ES - STI

Préciser dans chaque cas si les événements $\rm A$ et $\rm B$ sont indépendants:

$\rm P(A \cap B) = 0,36$ et $\rm P(A) = 0,4$ et $\rm P(B) = 0,9$.
$\rm P(A \cap B) = 0,4$ et $\rm P(A) = 0,5$ et $\rm P(\overline{B}) = 0,2$.
$\rm P(A \cup B) = 0,8$ et $\rm P(A) = 0,6$ et $\rm P(B) = 0,4$.

Exercice 7: Probabilités conditionnelles - Événements indépendants - Première spécialité maths S - ES - STI

Dans son aquarium, Manon a des poissons mâles et femelles, colorés ou non. On choisit un poisson au hasard. On considère les événements :
• M : « Le poisson est un mâle.»
• C : « Le poisson est coloré.»
La situation est représentée par l'arbre ci-dessous :

Les événements M et C sont-ils indépendants ?

Exercice 8: Probabilités conditionnelles - Événements indépendants - Première spécialité maths S - ES - STI

On lance deux dés bien équilibrés à $6$ faces numérotées de $1$ à $6$, un bleu et un rouge.
On note $\rm{A}$ l'événement «le dé bleu donne $1$» et $\rm{B}$ l'événement «la somme des dés donne $7$».
Montrer que $\rm{A}$ et $\rm{B}$ sont indépendants.

Exercice 9: Probabilités conditionnelles - Événements indépendants - Première spécialité maths S - ES - STI

Dans l'urne ci-dessous, il y a des jetons numérotés de différentes couleurs:

On tire au hasard un jeton dans cette urne. On considère les évènements suivants:
R: « le jeton tiré est rouge »,
B: « le jeton tiré est bleu »
I: « le numéro du jeton tiré est impair »

Les évènements R et I sont-ils indépendants?
Les évènements B et I sont-ils indépendants?

Exercice 10: Condition pour que deux évènements soient indépendants - Première spécialité maths S - ES - STI

Dans l'urne ci-dessous, il y a des jetons numérotés de différentes couleurs:

On tire au hasard un jeton dans cette urne. On considère les évènements suivants:
B : « le jeton tiré est bleu »
I : « le numéro du jeton tiré est impair »

Les évènements B et I sont-ils indépendants?
Combien faut-il rajouter de jetons bleus numérotés 1 pour que les évènements B et I soient indépendants?

Tous les niveaux couverts

Collège

Lycée

Supérieur

Manuels scolaires pour lesquels j'ai réalisé les vidéos

Jaicompris.com — dans la presse et les médias

Prêt à transformer ton apprentissage ?

Rejoins des milliers d'élèves qui ont déjà amélioré leurs résultats en mathématiques

Ce site ne convient pas aux enfants de moins de 36 mois, sauf s'ils insistent vraiment.
Ne pas dépasser la dose prescrite.
Posologie: 1 fois/jour la semaine avant le contrôle.
L'efficacité du traitement dépend d'une prise régulière.
Effet secondaire: Peut procurer du plaisir surtout en cas de réussite !
En cas de persistance des difficultés, arrêter le traitement pendant une nuit, puis reprendre le lendemain.

Site jaicompris 100% gratuit avec accès illimité aux vidéos et exercices

Académie de Poitiers – page mathématiques

Icône humoristique : satisfait ou remboursé, mais gratuit