Dans ce cours de géométrie dans l'espace destiné aux élèves de
Terminale spécialité mathématiques, vous allez apprendre à déterminer le
projeté orthogonal d'un point sur un
plan dans l'espace. Cette notion repose sur l'idée de
perpendicularité et permet notamment de calculer la
distance d'un point à un plan.
Pour cela, on utilisera la notion de vecteur normal à un plan ainsi que le
produit scalaire dans l'espace vus en Terminale spécialité mathématiques.
De nombreux
exercices type bac corrigés en vidéo
vous permettront de vous entraîner et de vérifier votre compréhension tout au long du chapitre afin de
vous préparer au contrôle.
Conseil important : penser à faire des schémas, cela aide beaucoup car
cela permet
de bien visualiser la situation dans l'espace.
Dans tout le chapitre, on est dans un repère orthonormé
Cours Projeté orthogonal d'un point sur un
plan
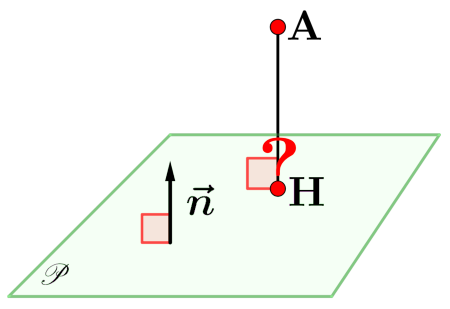
📌 Le projeté orthogonal d'un point A sur un plan est
le point H qui est à l'intersection du plan et de la droite passant par A orthogonale au
plan
-
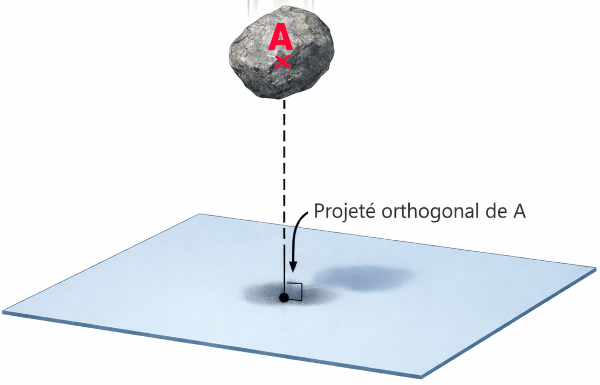
Pour bien comprendre la notion de projeté orthogonal :
Imaginez qu'on lâche une pierre qui tombe
verticalement sur un plan (le sol). Là où la
pierre touche le sol, se trouve le projeté
orthogonal
-
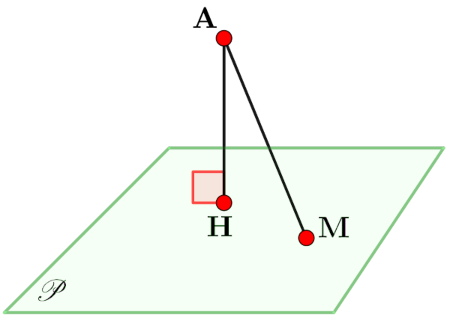
Le projeté orthogonal de A est le point du plan le plus
proche
de A

Soit H le projeté orthogonal de A sur le plan $\mathscr{P}$. H est le point du plan
$\mathscr{P}$ le plus proche de A.
Ce qui signifie que si on choisit un point M quelconque du plan $\mathscr{P}$, on a
: $\rm AM\geqslant AH$
📌 Comment trouver les coordonnées du point H projeté orthogonal
d'un point A sur un plan $\mathscr{P}$

-
On trouve un vecteur normal $\boldsymbol{\vec n}$ du
plan $\mathscr{P}$
d'intersection

Si un plan $\mathscr{P}$ a pour équation cartésienne
$\boldsymbol{{\color{red}a}x+{\color{green}b}y+{\color{magenta}{c}}z+d=0}$,
on en déduit que
le vecteur $\boldsymbol{\vec{n}\left(
\begin{array}{c}
{\boldsymbol{\color{red}a}} \\
{\boldsymbol{\color{green}b}}\\
{\boldsymbol{\color{magenta}{c}}}\\
\end{array}
\right)}$ est un vecteur normal à ce plan $\mathscr{P}$.
-
On note $\mathscr{D}$ la droite passant $\rm A$ et
orthogonale à $\mathscr{P}$. On
trouve une représentation paramétrique de cette droite
$\mathscr{D}$

Comme la droite $\mathscr{D}$ est orthogonale au plan $\mathscr{P}$, tout
vecteur normal du plan est vecteur directeur de la droite $\mathscr{D}$.
Donc la droite $\mathscr{D}$ passe par le point ${\rm A}(x_{\rm A};y_{\rm
A};z_{\rm A})$ et a pour vecteur
directeur $\vec n$.
On en déduit une représentation paramétrique de
${\mathscr{D}:\left\{
\begin{array}{l}
x=x_{\rm A}+a\times t \\
y=y_{\rm A}+b\times t\\
z=z_{\rm A}+c\times t\\
\end{array}
\right.\text{ où }t\in \mathbb{R}}$

où a,b et c sont les coordonnées d'un vecteur normal à $\mathscr{P}$
-
On résout le système formé par
l'équation du plan donnée dans
l'énoncé et les trois équations de la représentation paramétrique de la droite
$\mathscr{D}$

Il faudra résoudre un système de ce genre :
${\left\{
\begin{array}{l}
3{\color{red}x}-{\color{green}y}+2{\color{magenta}z}+1=0 \\
{\color{red}x}=2+3t \\
{\color{green}y}=1- t\\
{\color{magenta}z}=4-3 t\\
\end{array}
\right.}$
📌 La méthode
On remplace dans la
première équation ${\color{red}x}$, ${\color{green}y}$ et
${\color{magenta}z}$ respectivement par
$\color{red}{2+3t}$, $\color{green}{1-t}$ et $\color{magenta}{4-3t}$ et
on obtient:
${\left\{
\begin{array}{l}
3(\color{red}{2+3t})-(\color{green}{1-t})+2(\color{magenta}{4-3t})+1=0 \\
x=2+3t \\
y=1- t\\
z=4-3 t\\
\end{array}
\right.}$
Grâce à la première équation, on trouve la valeur de $t$. Puis on
remplace cette valeur de $t$ dans les 3 autres équations et on trouve
$x$, $y$ et $z$ qui sont les coordonnées du projeté orthogonal.
✏️ Exercice type
Soit $\rm H$ le projeté
orthogonal du point $\rm A(2;5;-1)$ sur le plan $\mathscr{P}$ d'équation ${x-2y+3z-17=0}$.
Déterminer les coordonnées du point
$\rm H$ 
-
On trouve un vecteur normal $\boldsymbol{\vec n}$ du
plan $\mathscr{P}$.
Comme $x-2y+3z-17=0$, le vecteur $\vec n(1;-2;3)$ est normal au plan
$\mathscr{P}$
-
On trouve une représentation paramétrique de la droite $\mathscr{D}$ passant
$\rm A$ et orthogonal à $\mathscr{P}$ :
${\mathscr{D}:\left\{
\begin{array}{l}
x=2+ t \\
y=5-2t\\
z=-1+3 t\\
\end{array}
\right.\text{ où }t\in \mathbb{R}}$
-
On résout le système formé par l'équation du plan et les trois équations de la
représentation paramétrique de la droite
$\mathscr{D}$ :
${\left\{
\begin{array}{l}
{\color{red}x}-2{\color{green}y}+3{\color{magenta}z}-17=0 \\
{\color{red}x}=\color{red}{2+t} \\
{\color{green}y}=\color{green}{5- 2t}\\
{\color{magenta}z}=\color{magenta}{-1+3 t}\\
\end{array}
\right.}$
${\Leftrightarrow \left\{
\begin{array}{l}
{\color{red}{2+t}}-2({\color{green}{5-2t}})+3({\color{magenta}{-1+3t}})-17=0 \\
{\color{red}x}=2+t \\
{\color{green}y}=5- 2t\\
{\color{magenta}z}=-1+3 t\\
\end{array}
\right.}$
${\Leftrightarrow \left\{
\begin{array}{l}
14t-28=0 \\
{x}=2+t \\
{y}=5- 2t\\
{z}=-1+3 t\\
\end{array}
\right.}$
${\Leftrightarrow \left\{
\begin{array}{l}
t=2 \\
{x}=4 \\
{y}=1\\
{z}=5\\
\end{array}
\right.}$
Conclusion : Le point H a pour coordonnées $(4;1;5)$
👉 Techniques à connaître en exercices