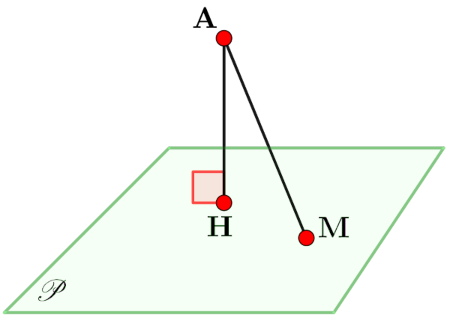
Distance d'un point à un plan | Géométrie dans l'espace
Terminale spécialité maths
1000 cours en vidéo
2000 exercices corrigés en vidéo
2000 abonnés