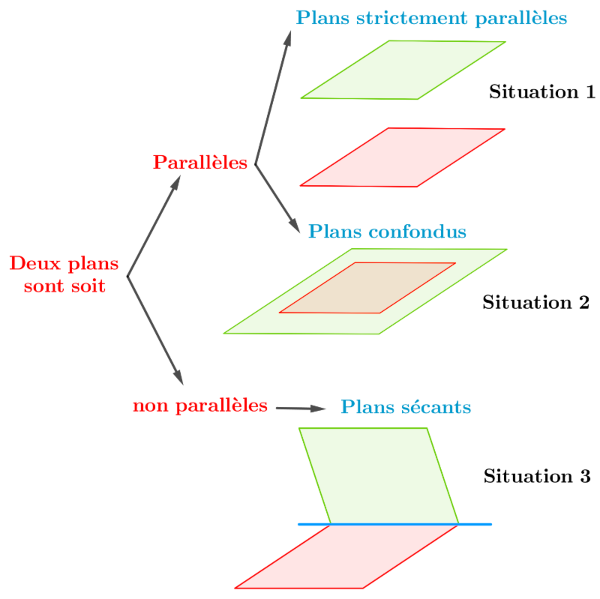
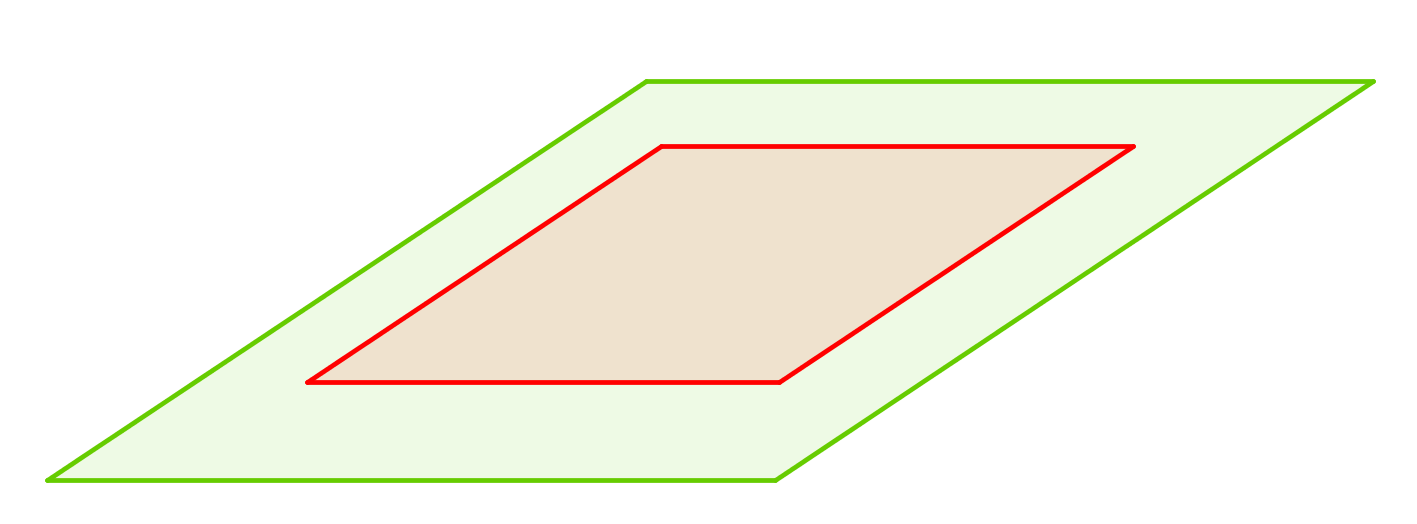
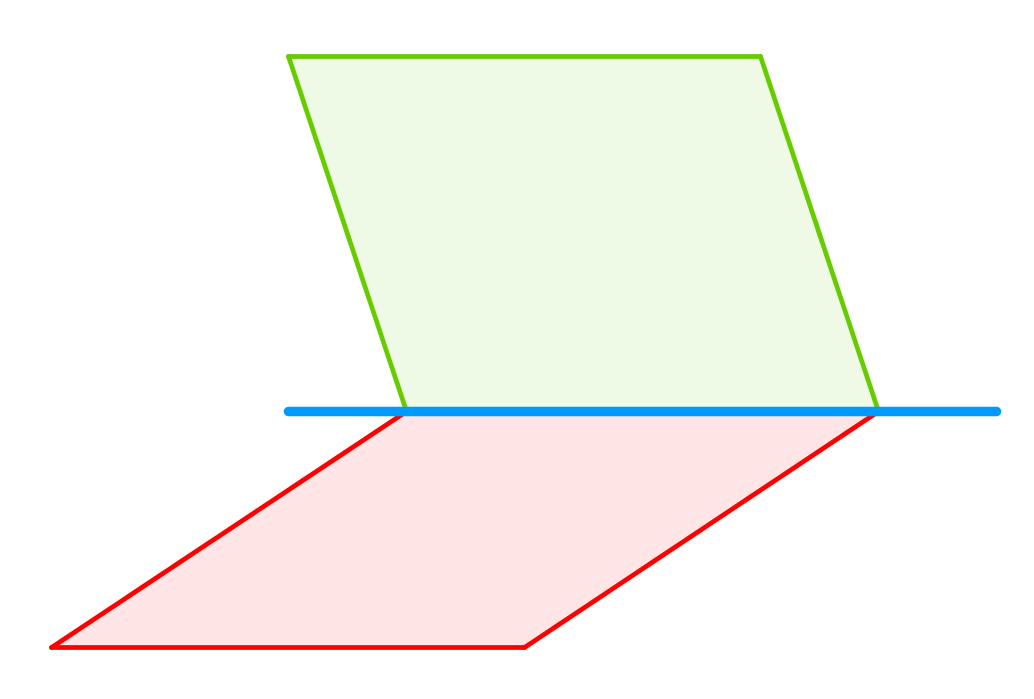
Position relative de 2 plans : intersection, sécant, parallèle ou confondu | Géométrie dans l'espace
Terminale spécialité maths
1000 cours en vidéo
2000 exercices corrigés en vidéo
2000 abonnés