Intersection plan & droite - Sécant Parallèle - Incluse - Position relative

Dans ce cours de géométrie dans l'espace destiné aux élèves de Terminale spécialité mathématiques, vous allez apprendre à déterminer la position relative d'une droite et d'un plan, c'est à dire à savoir si une droite est parallèle, incluse ou sécante à un plan, ainsi que les méthodes pour déterminer le point d'intersection d'une droite et d'un plan.

Conseil important : penser à faire des schémas, ça aide beaucoup car cela permet de bien visualiser la situation.

Dans tout le chapitre, on est dans un repère orthonormé

Cours - Position relative de droite et plan

📌 Il y a 3 situations possibles

Soit la droite est parallèle au plan. Il y a alors deux possibilités :
- Soit la droite est strictement parallèle au plan (Situation 1)
  
  La droite est parallèle au plan mais à l'extérieur du plan.
- Soit la droite est incluse dans le plan (Situation 2)
Soit la droite n'est pas parallèle au plan (Situation 3)

Dans ce cas la droite coupe le plan en un point unique. On dit alors que la droite est sécante au plan.

📌 En exercice, pour étudier la position relative d'une droite et d'un plan :

On trouve un vecteur directeur $\boldsymbol{\vec u}$ de la droite et un vecteur normal $\boldsymbol{\vec n}$ du plan.
On regarde si $\boldsymbol{\vec n}$ et $\boldsymbol{\vec u}$ sont orthogonaux
Pour cela, on calcule le produit scalaire $\vec n\cdot \vec u$
- Si $\boldsymbol{\vec n\cdot \vec u=0}$ alors la droite est parallèle au plan
  
  alors $\vec n$ et $\vec u$ sont orthogonaux donc la droite (rose) est parallèle au plan (marron), comme sur ce schéma :
  
  Il y a alors 2 possibilités :
  
  Soit la droite est strictement parallèle au plan (situation 1)
  
  Soit la droite est incluse dans le plan (situation 2)
  
  👉 Pour savoir si la droite est incluse dans le plan (situation 1) ou strictement parallèle au plan (situation 2)
  On prend un point de la droite et on regarde si ses coordonnées vérifient l'équation du plan :
  
  Si c'est le cas, la droite est incluse dans le plan (situation 2)
  
  Sinon la droite est strictement parallèle au plan (situation 1)
- Si $\boldsymbol{\vec n\cdot \vec u\ne 0}$ alors la droite est sécante au plan
  
  alors $\vec n$ et $\vec u$ ne sont pas orthogonaux et donc la droite (rose) n'est pas parallèle au plan (marron). Donc la droite (rose) est sécante au plan (marron) comme sur ce schéma :
  
  👉 Ensuite pour trouver le point d'intersection de la droite et du plan
  On résout le système formé par la représentation paramétrique de la droite et l'équation du plan comme dans
  ✏️ Exemple 3
  .

✏️ Exemple 1

Droite incluse dans un plan :

Soit $\rm A(3;1;0)$ et $\rm B(1;4;12)$. Montrer que la droite $\rm (AB)$ est incluse dans le plan $\mathscr{P}$ d'équation $3x-2y+z-7=0$

Dans l'équation du plan $\mathscr{P}$, on remplace $x$, $y$ et $z$ par les coordonnées de $\rm A$ :
$3\times 3-2\times 1+0-7={\color{red}0}$
On trouve ${\color{red}0}$, donc le point $\rm A$ appartient au plan $\mathscr{P}$.

Dans l'équation du plan $\mathscr{P}$, on remplace $x$, $y$ et $z$ par les coordonnées de $\rm B$ :
$3\times 1-2\times 4+12-7={\color{red}0}$
on trouve ${\color{red}0}$, donc le point $\rm B$ appartient au plan $\mathscr{P}$.

Comme les points $\rm A$ et $\rm B$ appartiennent $\mathscr{P}$, la droite $\rm (AB)$ est incluse dans le plan $\mathscr{P}$.

✏️ Exemple 2

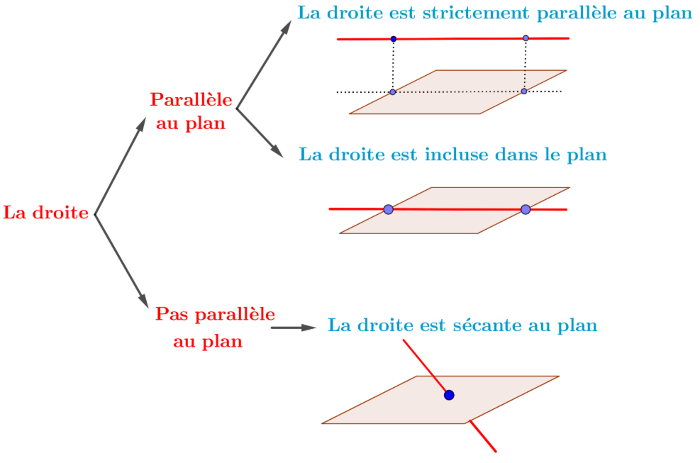
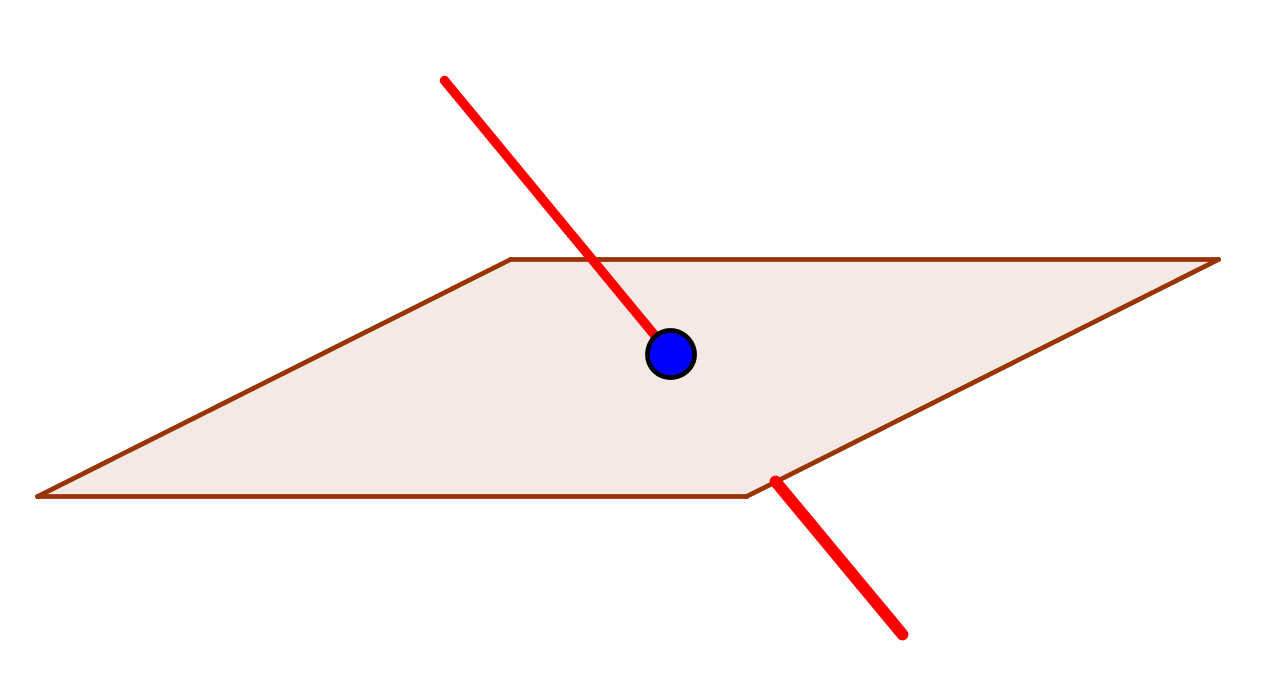
Droite strictement parallèle à un plan :

Soit $\rm A(2;-1;3)$ et $\rm B(5;4;7)$. Montrer que la droite $\rm (AB)$ est strictement parallèle au plan $\mathscr{P}$ d'équation $5x-7y+5z-8=0$

On a $\overrightarrow{\rm AB}\left( \begin{array}{c} 3 \\ 5\\ 4\\ \end{array} \right)$ et le vecteur $\vec n\left( \begin{array}{c} 5 \\ -7\\ 5\\ \end{array} \right)$ est normal au plan $\mathscr{P}$.
$\overrightarrow{\rm AB}\cdot \vec{n}=3\times 5+5\times (-7)+4\times 5\\ \phantom{\overrightarrow{\rm AB}\cdot \vec{n}}=0$
Donc la droite $\rm (AB)$ est parallèle au plan $\mathscr{P}$. Maintenant regardons si la droite $\rm (AB)$ est strictement parallèle ou incluse dans le plan $\mathscr{P}$. Pour cela, remplaçons les coordonnées du point $\rm A(2;-1;3)$ dans l'équation du plan $\mathscr{P}$ :
$5\times 2-7\times (-1)+5\times 3-8=24\ne 0$
Donc le point $\rm A$ n'appartient pas au plan $\mathscr{P}$. Donc la droite $\rm (AB)$ n'est pas incluse dans le plan $\mathscr{P}$. Donc la droite $\rm (AB)$ est strictement parallèle au plan $\mathscr{P}$.

✏️ Exemple 3

Droite sécante à un plan et point d'intersection :

Soit $\rm A(2;-1;3)$ et $\rm B(5;4;0)$. Montrer que la droite $\rm (AB)$ est sécante au plan $\mathscr{P}$ d'équation $x-2y+z-1=0$ et déterminer leur point d'intersection

On a $\overrightarrow{\rm AB}\left( \begin{array}{c} 3 \\ 5\\ -3\\ \end{array} \right)$ et le vecteur $\vec n\left( \begin{array}{c} 1 \\ -2\\ 1\\ \end{array} \right)$ est normal au plan $\mathscr{P}$.
$\overrightarrow{\rm AB}\cdot \vec{n}=3\times 1+5\times (-2)-3\times 1\\ \phantom{\overrightarrow{\rm AB}\cdot \vec{n}}=-10\ne 0$
Donc la droite $\rm (AB)$ est sécante au plan $\mathscr{P}$.
On détermine une représentation paramétrique de la droite $\rm (AB)$:
$\left\{ \begin{array}{l} x=2+3t \\ y=-1+5t\\ z=3-3t\\ \end{array} \right.$ où $t\in \mathbb{R}$

Pour déterminer le point d'intersection de la droite et du plan, on résout le système

Pour résoudre ce système, on remplace dans la dernière équation $x$ par $2+3t$ , $y$ par $-1+5t$ et $z$ par $3-3t$.
Du coup, dans la dernière équation, on n'a plus qu'une seule inconnue $t$. On trouve la valeur de $t$ qui est $\dfrac 35$.
Puis on remplace partout $t$ par sa valeur $\dfrac 35$ et on obtient les valeurs de $x$, $y$ et $z$.

$\left\{ \begin{array}{l} {\color{red}x}=2+3t \\ {\color{green}y}=-1+5t\\ {\color{blue}z}=3-3t\\ {\color{red}x}-2{\color{green}y}+{\color{blue}z}-1=0\\ \end{array} \right.$ $\Leftrightarrow\left\{ \begin{array}{l} x=2+3t \\ y=-1+5t\\ z=3-3t\\ {\color{red}{2+3t}}-2{\color{green}{(-1+5t)}}+{\color{blue}{3-3t}}-1=0\\ \end{array} \right.$ $\Leftrightarrow\left\{ \begin{array}{l} x=\dfrac{19}5 \\ y=2\\ z=\dfrac 65\\ t=\dfrac 35\\ \end{array} \right.$
Donc le point d'intersection de la droite et du plan a pour coordonnées $\left(\dfrac {19}5;2;\dfrac 65\right)$.

👉 Techniques à connaître en exercices

Montrer qu'une droite est orthogonale à un
plan
1. On trouve les coordonnées d'un vecteur $\vec n$ normal au plan.
2. On trouve les coordonnées d'un vecteur $\vec u$ directeur de la droite.
3. On regarde Si $\vec n$ et $\vec u$ sont colinéaires
  Pour cela, on regarde si les coordonnées de $\vec n$ et $\vec u$ sont proportionnelles.
  Si c'est le cas, alors la droite est orthogonale au plan.
  
  Sinon la droite n'est pas orthogonale au plan.
Montrer qu'une droite est orthogonale au plan
$(\rm ABC)$
1. On trouve les coordonnées d'un vecteur $\vec u$ directeur de la droite.
2. On regarde si $\vec u \cdot \overrightarrow{{\rm AB}}=0$ et $\vec u \cdot \overrightarrow{{\rm AC}}=0$
  Si c'est le cas, alors la droite est orthogonale au plan.
  
  Sinon la droite n'est pas orthogonale au plan.
Montrer qu'une droite est parallèle à un
plan
1. On trouve les coordonnées d'un vecteur $\vec n$ normal au plan.
2. On trouve les coordonnées d'un vecteur $\vec u$ directeur de la droite.
3. On regarde Si $\vec n$ et $\vec u$ sont orthogonaux
  Pour cela, on calcule le produit scalaire $\vec n \cdot \vec u$ et on regarde si ce produit scalaire vaut $0$ ou pas.
  Si c'est le cas, alors la droite est parallèle au plan.
  
  Sinon la droite n'est pas parallèle au plan.
Savoir si une droite est incluse dans un
plan
1. On trouve 2 points de la droite et on regarde si ces deux points sont dans le plan
  Pour cela, on remplace dans l'équation du plan $x$, $y$, $z$ par les coordonnées de chaque point et on regarde à chaque fois si l'équation est vérifiée.
2. Si les deux points appartiennent au plan alors la droite est incluse dans le plan.
  Sinon la droite n'est pas incluse dans le plan.

✏️ EXERCICE Très IMPORTANT

14:11

Position relative droite plan

📌 COURS

14:35

Les questions qui tombent en exercice

Exercice 1: Étudier la position relative d'une droite et d'un plan - parallèle sécante - terminale spé maths

L'espace est muni d'un repère orthonormé $({\rm O},~\vec i,~\vec j,~\vec k)$. On considère les points ${\rm A}(-3 ; 1 ; 4)$ et ${\rm B}(1; 5; 2)$ et le plan $\mathscr{P}$ d'équation cartésienne $-2x -y +z -3 = 0$.
La droite $\rm (AB)$ est-elle :

incluse dans le plan $\mathscr{P}$ ?
strictement parallèle au plan $\mathscr{P}$ ?
orthogonale au plan $\mathscr{P}$ ?
sécante et non orthogonale au plan $\mathscr{P}$ ?
Si oui, déterminer les coordonnées de leur point d'intersection.

Exercice 2: Déterminer l'intersection d'une droite et d'un plan - géométrie dans l'espace - terminale spé maths

On se place dans un repère orthonormé ($O; \vec i;\vec j; \vec k$).
On considère la droite $\mathscr{D}$ de représentation paramétrique $\left\{ \begin{array}{l} x=1-t \\ y=2t\\ z=-1\\ \end{array} \right.$ où $t\in \mathbb{R}$
Le plan $\mathscr{P}$ a pour équation cartésienne $2x-y+z-3=0$.

Justifier que $\mathscr{P}$ et $\mathscr{D}$ sont sécants en un point I.
Déterminer les coordonnées de I.

Exercice 3: équation cartésienne de plan - Bac 2025 Spécialité Maths ♦ Amérique du Nord

Dans l'espace muni d'un repère orthonormé, on considère :

le plan $\mathscr{P}$ d'équation cartésienne $2x-y+3z+6 = 0$
les points $\rm A(2 ; 0 ; -1)$ et $\rm B(5 ; -3 ; 7)$

Le plan $\mathscr{P}$ et la droite $\rm (AB)$ sont-ils parallèles ?

Exercice 4: équation cartésienne de plan - Bac 2025 Spécialité Maths ♦ Amérique du Nord

Deux cubes d'arête 1, sont disposés comme indiqué sur la figure ci-dessous :

M est le milieu du segment [GK].
La droite (DL) est-elle perpendiculaire au plan (FMI) ?

Exercice 5: Équation de plan et section d'un cube par un plan - Bac S Pondichéry 2017 - terminale spé maths

$\rm ABCDEFGH$ est un cube.
Dans le repère $\left( \rm A;\overrightarrow{\rm AB};\overrightarrow{\rm AD};\overrightarrow{\rm AE}\right)$, on note $\mathcal{P}$ le plan d'équation $x + \dfrac{1}{2} y +\dfrac{1}{3}z -1 = 0$.

Reproduire la figure ci-dessous au centre d'une feuille blanche puis construire la section du cube par le plan $\mathcal{P}$, en justifiant.

Exercice 6: Distance d'un point à une droite par 2 méthodes - Bac S Pondichéry 2017 - terminale spé maths

Dans un repère orthonormé ($O; \vec i;\vec j; \vec k$), on considère le point A(-1;1;2) et la droite $\mathscr{D}$ de représentation paramétrique : $\left\{ \begin{array}{l} x=t \\ y=-1\\ z=1-2t\\ \end{array} \right.$ où $t\in \mathbb{R}$.

L'objectif de cet exercice est de déterminer la distance du point A à la droite $\mathscr{D}$, c'est à dire la plus petite des longueurs AM lorsque M décrit la droite $\mathscr{D}$.

Méthode 1

On considère la fonction $f$ définie sur $\mathbb{R}$ par $f(t)=AM$ où M est un point de $\mathscr{D}$ de paramètre $t$. Déterminer $f(t)$ en fonction de $t$ puis le minimum de $f$. Conclure.

Méthode 2

1. Déterminer une équation cartésienne du plan $\mathscr{P}$ perpendiculaire à $\mathscr{D}$ passant par A.
2. Déterminer les coordonnées du point H, intersection de $\mathscr{P}$ et $\mathscr{D}$.
3. Conclure.

Exercice 7: Perpendiculaire commune à deux droites de l'espace - Bac S - terminale spé maths

Dans un repère orthonormé, on considère la droite $\mathscr{D}_1$ passant par $A_1$(-1;0;-1) et de vecteur directeur
$\vec{u}_1$(1;2;3), et la droite $\mathscr{D}_2$ de représentation paramétrique: $\left\{ \begin{array}{l} x=1+t\\ y=-2t\\ z=2\\ \end{array} \right.$ où $t\in\mathbb{R}$.

Déterminer un vecteur directeur de $\mathscr{D}_2$, noté $\vec{u}_2$.
Déterminer les coordonnées d'un vecteur $\vec v$ non nul orthogonal à $\vec{u}_1$ et à $\vec{u}_2$.
On considère le plan $\mathscr{P}$($A_1;\vec{u}_1;\vec v$).
1. Montrer que le vecteur $\vec n$(17;-22;9) est normal à $\mathscr{P}$. En déduire une équation cartésienne de $\mathscr{P}$.
2. Déterminer les coordonnées du point I, intersection de $\mathscr{P}$ et $\mathscr{D}_2$.
3. Démontrer que la droite $\Delta$ passant par I et de vecteur directeur $\vec v$ est perpendiculaire à $\mathscr{D}_1$ et $\mathscr{D}_2$.

Position relative de droite et plan : intersection, sécante, parallèle ou incluse | Géométrie dans l'espace

Cours - Position relative de droite et plan

📌 Il y a 3 situations possibles

📌 En exercice, pour étudier la position relative d'une droite et d'un plan :

✏️ Exemple 3

✏️ Exemple 1

✏️ Exemple 2

✏️ Exemple 3

👉 Techniques à connaître en exercices

Montrer qu'une droite est orthogonale à un

Montrer qu'une droite est orthogonale au plan

Montrer qu'une droite est parallèle à un

Savoir si une droite est incluse dans un

Position relative droite plan

Les questions qui tombent en exercice

Exercice 1: Étudier la position relative d'une droite et d'un plan - parallèle sécante - terminale spé maths

Exercice 2: Déterminer l'intersection d'une droite et d'un plan - géométrie dans l'espace - terminale spé maths

Exercice 3: équation cartésienne de plan - Bac 2025 Spécialité Maths ♦ Amérique du Nord

Exercice 4: équation cartésienne de plan - Bac 2025 Spécialité Maths ♦ Amérique du Nord

Exercice 5: Équation de plan et section d'un cube par un plan - Bac S Pondichéry 2017 - terminale spé maths

Exercice 6: Distance d'un point à une droite par 2 méthodes - Bac S Pondichéry 2017 - terminale spé maths

Exercice 7: Perpendiculaire commune à deux droites de l'espace - Bac S - terminale spé maths

Tous les niveaux couverts

Lycée

Supérieur

Manuels scolaires pour lesquels j'ai réalisé les vidéos

Jaicompris.com — dans la presse et les médias

Prêt à transformer ton apprentissage ?