
jaicompris.com
Cours et exercices corrigés en vidéo


|
Sens de variation d'une suite |

|

 Avec les suites du type $u_n=f(n)$
Avec les suites du type $u_n=f(n)$

 En calculant $u_{n+1}\div {u_n}$
En calculant $u_{n+1}\div {u_n}$

 Exercice type
Exercice type
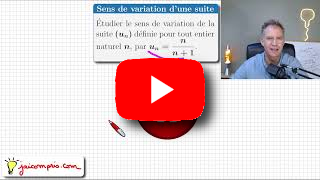 Exercice type
Exercice type
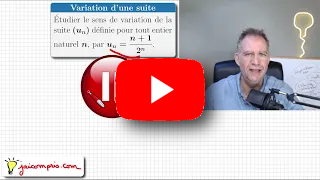
 Exercice type
Exercice type
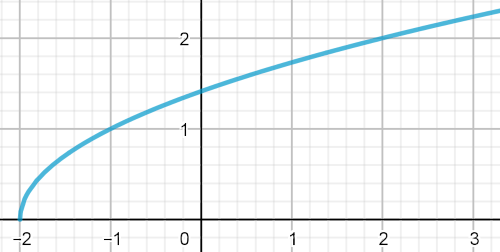
 Suite croissante
Suite croissante















Rejoins des milliers d'élèves qui ont déjà amélioré leurs résultats en mathématiques