


|
Produit scalaire en Première spé maths
|

|
Le produit scalaire est un outil fondamental en mathématiques, utilisé pour calculer des angles, des longueurs et des projections entre vecteurs. Dans cette page, nous allons voir comment calculer le produit scalaire, comprendre ses formules et ses propriétés, et découvrir des exercices corrigés sur le produit scalaire pour mieux maîtriser ce concept. Que vous soyez en Première spé maths ou simplement curieux, cette page vous guidera pas à pas pour tout savoir sur le produit scalaire.







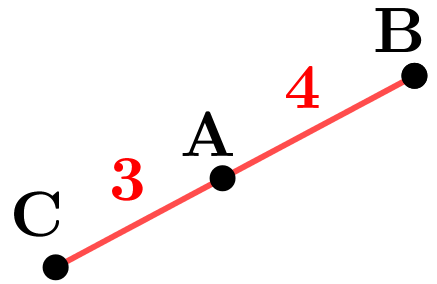 $\color{red}{\textbf{b.
}} $
$\color{red}{\textbf{b.
}} $ 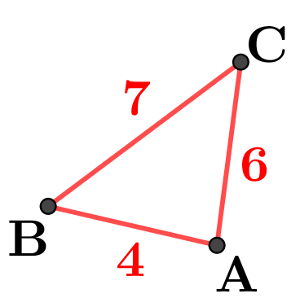 $\color{red}{\textbf{c.
}} $
$\color{red}{\textbf{c.
}} $ 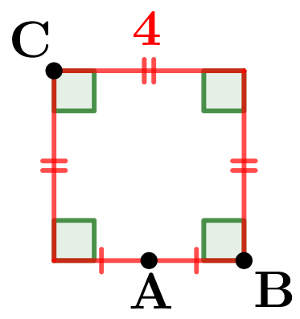 $\color{red}{\textbf{d.
}} $
$\color{red}{\textbf{d.
}} $ 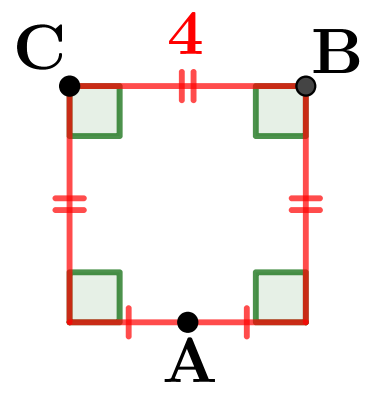 $\color{red}{\textbf{e.
}} $
$\color{red}{\textbf{e.
}} $  $\color{red}{\textbf{f.
}} $
$\color{red}{\textbf{f.
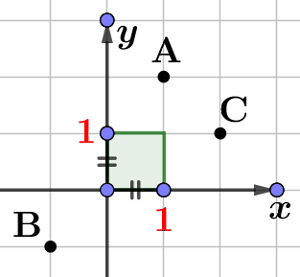
}} $ 






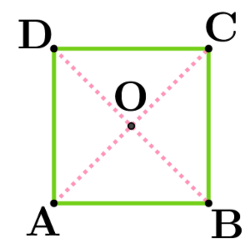

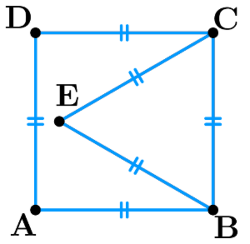

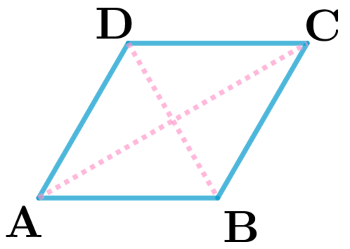


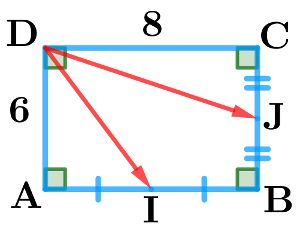





Rejoins des milliers d'élèves qui ont déjà amélioré leurs résultats en mathématiques