Racine carrée d'un nombre réel

Conseils

Racine carrée d'un nombre réel

Exercice rapide

pour savoir calculer une racine carrée en 3 min !

Cours complet

La racine carrée

, expliquée en vidéo

•

Définition de la racine carrée

•

Exemples

•

Ne pas confondre $\boldsymbol{{{\sqrt a}^~}^2}$ et $\boldsymbol{\sqrt{a^2}}$

Dans ${{\sqrt a}^~}^2$
$a$ doit être positif
Car on calcule d'abord la racine. Et ensuite le carré!
Dans $\sqrt{a^2}$
$a$ peut être positif ou négatif !
Car on calcule d'abord le carré. Et ensuite la racine !

${{{\sqrt a}^~}^2=a}$

${\sqrt {a^2}=|a|}$

Cours

Règles de calcul avec des racines carrées

, expliquées en vidéo

•

${\sqrt{ab}}$

Propriété $\boldsymbol{\sqrt{ab}=\sqrt a \times \sqrt b}$

Formule pratique pour calculer des "grosses" racines

Penser à utiliser cette formule dans les deux sens

Exemple $\sqrt{4900}$

Cours

Démonstration de $\boldsymbol{\sqrt{ab}=\sqrt a \times \sqrt b}$

, en vidéo

•

${\sqrt{\dfrac ab}}$

•

${ \sqrt{a+b}}$

Exercice 1: Calculer avec des racines carrées - collège seconde mathématiques

Sans calculatrice, calculer:

$\color{red}{\textbf{a. }} \sqrt{4}$ $\color{red}{\textbf{b. }} \sqrt{16}$ $\color{red}{\textbf{c. }} \sqrt {49}$

Exercice 2: Calculer avec des racines carrées - Simplifier - seconde mathématiques

Sans utiliser de calculatrice, calculer:

$\color{red}{\textbf{a. }} \sqrt{9}$ $\color{red}{\textbf{b. }} \sqrt{25}$ $\color{red}{\textbf{c. }} \sqrt {100}$ $\color{red}{\textbf{d. }} \sqrt {64}$ $\color{red}{\textbf{e. }} \sqrt {1}$ $\color{red}{\textbf{f. }} \sqrt {0}$

Exercice 3: Simplifier des racines carrées - seconde - mathématiques

Sans utiliser de calculatrice, écrire les nombres suivants sans racine carrée:

$\color{red}{\textbf{a. }} {\sqrt {41}}^2$ $\color{red}{\textbf{b. }} \sqrt{2,8^2}$ $\color{red}{\textbf{c. }} \sqrt{20}\times \sqrt 5$ $\color{red}{\textbf{d. }} \sqrt{(-6)^2}$ $\color{red}{\textbf{e. }} 2\sqrt{2}\times \sqrt 4\sqrt{18}$ $\color{red}{\textbf{f. }} \sqrt{7^{18}}$

Exercice 4: Calculer avec des racines carrées - Simplifier - Fraction - seconde mathématiques

Sans utiliser de calculatrice, écrire les nombres suivants sans racine carrée:

$\color{red}{\textbf{a. }} \sqrt{3600}$ $\color{red}{\textbf{b. }} \sqrt{0,64}$ $\color{red}{\textbf{c. }} \left( 3\sqrt 5 \right)^2$ $\color{red}{\textbf{d. }} \sqrt{0,01}$

Exercice 5: Calculer avec des racines carrées - Simplifier - Fraction - seconde mathématiques

Simplifier sans utiliser de calculatrice: $\dfrac{\sqrt{5}\times \sqrt{5}\times\sqrt{5}\times\sqrt{5}\times \sqrt{5} }{\sqrt{5}+\sqrt{5}+\sqrt{5}+\sqrt{5}+\sqrt{5}}$

Exercice 6: encadrer une racine carrée entre 2 entiers consécutifs - Calcul mental - seconde - mathématiques

Encadrer les nombres suivants entre deux entiers consécutifs sans utiliser de calculatrice:

$\color{red}{\textbf{a. }} \sqrt{29}$ $\color{red}{\textbf{b. }} \sqrt{11}$ $\color{red}{\textbf{c. }} \sqrt{85}$

Exercice 7: encadrer une racine carrée entre 2 entiers consécutifs - Calcul mental - seconde - mathématiques

Encadrer les nombres suivants entre deux entiers consécutifs sans utiliser de calculatrice:

$\color{red}{\textbf{a. }} \sqrt{7}$ $\color{red}{\textbf{b. }} \sqrt{20}$ $\color{red}{\textbf{c. }} \sqrt{75}$ $\color{red}{\textbf{c. }} \sqrt{200}$

Exercice 8: Comparer deux nombres avec racine carré - seconde - mathématiques

Parmi les nombres $3\sqrt 2 $ et $2\sqrt 3$, lequel est le plus grand ? (Sans utiliser de calculatrice)

Exercice 9: Erreur sur les racines carrés - seconde - mathématiques

Rose affirme que $\sqrt{a+b}=\sqrt a+\sqrt b$ où $a$ et $b$ sont des nombres positifs. Expliquer pourquoi son affirmation est fausse.

Exercice 10: Écrire une racine carrée sous la forme $a\sqrt b$ - seconde - mathématiques

Sans utiliser de calculatrice, écrire les nombres suivants sous la forme $a\sqrt b$ avec $a$ et $b$ entiers et $b$ le plus petit possible:

$\color{red}{\textbf{a. }} \sqrt 8$ $\color{red}{\textbf{b. }} \sqrt{45}$ $\color{red}{\textbf{c. }} \sqrt{75}$ $\color{red}{\textbf{c. }} \sqrt{128}$

Exercice 11: Ecrire une racine carrée sous la forme $a\sqrt b$ - seconde - mathématiques

Sans utiliser de calculatrice, écrire les nombres suivants sous la forme $a\sqrt b$ avec $a$ et $b$ entiers et $b$ le plus petit possible:

$\color{red}{\textbf{a. }} \sqrt {12}$ $\color{red}{\textbf{b. }} \sqrt{1000}$ $\color{red}{\textbf{c. }} 2\sqrt 2\times 3\sqrt 6$

Exercice 12: Calculer avec des racines carrées - seconde - mathématiques

Sans utiliser de calculatrice, dire si les égalités suivantes sont vraies ou pas. Justifier.

$\color{red}{\textbf{a. }} \sqrt {\dfrac{160}{9}}=\dfrac 43 \sqrt {10}$ $\color{red}{\textbf{b. }} \dfrac 3{\sqrt 3}=\sqrt {3}$ $\color{red}{\textbf{c. }} \sqrt {6^2}=6$ $\color{red}{\textbf{c. }} \sqrt {6^2+8^2}=14$

Exercice 13: Calculer avec des racines carrées - seconde - mathématiques

Développer et réduire:

$\color{red}{\textbf{a. }} (\sqrt 3-1)^2$ $\color{red}{\textbf{b. }} (15-\sqrt 7)(\sqrt 7 -4)$ $\color{red}{\textbf{c. }} (\sqrt 5-\sqrt 2)$

Exercice 14: Savoir calculer avec des racines carrées - mathématiques - seconde

Écrire les expressions suivantes sous la forme $a\sqrt 3$ avec $a$ entier :

$\color{red}{\textbf{a. }} \sqrt{300}-\sqrt{12}-\sqrt{75}$ $\color{red}{\textbf{b. }} \dfrac {180}{\sqrt {108}}$

Exercice 15: Réduire une somme avec des racines carrées - seconde - mathématiques

Réduire au maximum les sommes suivantes:

$\color{red}{\textbf{a. }} \sqrt 2+\sqrt 8$ $\color{red}{\textbf{b. }} 2\sqrt 3+\sqrt{48}$ $\color{red}{\textbf{c. }} 3+2\sqrt{5}-1-\sqrt{45}$

Exercice 16: Calculer avec des racines carrées - Simplifier - Fraction

Écrire les expressions suivantes sous la forme $\sqrt a$ avec $a$ entier naturel:

$\color{red}{\textbf{a. }} 2\sqrt 3$ $\color{red}{\textbf{b. }} \dfrac {\sqrt {32}}4$ $\color{red}{\textbf{c. }} \sqrt{20}+\sqrt{20}$

Exercice 17: Racine carrée - mathématiques - seconde - quantité conjuguée

Écrire les expressions suivantes sans racine au dénominateur puis simplifier:

$\color{red}{\textbf{a. }} \dfrac 1{\sqrt 2}$ $\color{red}{\textbf{b. }} \sqrt 3+\dfrac 9{\sqrt 3}$ $\color{red}{\textbf{c. }} \dfrac 1{\sqrt 2 + \sqrt 3}$ $\color{red}{\textbf{d. }} \dfrac 2{\sqrt 5 -1}$

Exercice 18: Racine carrée - mathématiques - seconde - diagonale d'un carré - Théorème de Pythagore

Montrer que dans un carré de côté $a$, la longueur $d$ de la diagonale est donnée par la formule $d=\sqrt 2 a$.

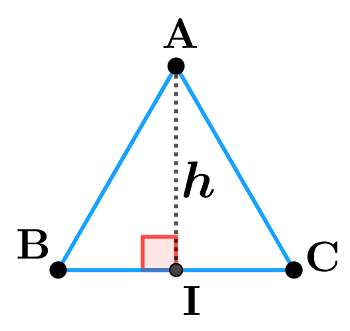
Exercice 19: Racine carrée - mathématiques - seconde - hauteur d'un triangle équilatéral

ABC est un triangle équilatéral de côté $a$.

Démontrer que $h=\dfrac {\sqrt 3}2 a$.

Exercice 20: Racine carrée & physique - inverser une formule - mathématiques - seconde

Inverser une formule avec racine $T=2\pi \sqrt{\dfrac Lg}$

Exercice 21: Racine carrée - problème - Tache complexe - mathématiques - seconde

ABCD est un rectangle. On sait de plus que AB=$\sqrt{300}-\sqrt{147}$ et BC=$\dfrac {\sqrt {150}}{\sqrt 2}-\sqrt{12}$.

Démontrer que ABCD est un carré.
Calculer l'aire de ABCD. Donner le résultat sous forme simplifiée.

Exercice 22: Démonstration Racine de 2 irrationnel - cours - mathématiques - seconde - racine carrée

L'objectif de cet exercice est de démontrer que racine de 2 est irrationnel.
On rappelle que: si $a^2$ est pair alors $a$ est pair.
Supposons que $\sqrt 2$ est rationnel, c'est à dire qu'il existe $p$ et $q$ entiers tels que: $\sqrt 2=\dfrac pq$ avec $\dfrac pq$ irréductible.

Démontrer qu'alors $p$ est pair.
En déduire que $q$ est pair.
Conclure.

Exercice 23: Algorithmique - python - valeur approchée de racine de 2 par balayage - mathématiques - seconde - racine carrée

Ecrire un programme en python pour déterminer par balayage un encadrement de racine de 2 à $10^{-3}$ près.

Exercice 24: Algorithmique - python - valeur approchée de racine de 2 par dichotomie - mathématiques - seconde - racine carrée

Ecrire un programme en python pour déterminer par dichotomie un encadrement de racine de 2 à $10^{-3}$ près.