| Cours
|
Exemple
|
Définition Dérivée
seconde

Dire qu'une fonction $f$ est deux fois
dérivable sur un
intervalle $\rm I$ signifie que $f$ est dérivable sur $\rm I$ et
que sa
dérivée $\boldsymbol{f'}$
est elle-même dérivable sur $\rm I$

Dans ce cas, la dérivée de $f'$ est notée
$\boldsymbol{f''}$ et est
appelée dérivée seconde de $f$.
|
Déterminer la dérivée seconde de la fonction $f$ définie sur
$\mathbb{R}$ par $f(x) = x^3 + 6x^2 - 3x + 1$.

$f$ est dérivable sur $\mathbb{R}$

Car $f$ est une fonction
polynôme donc dérivable sur
$\mathbb{R}$.
et pour tout réel $x$,
$f'(x)=3x^2+12x-3$.
$f'$ est dérivable sur $\mathbb{R}$ 
Car $f'$ est une fonction
polynôme donc dérivable sur
$\mathbb{R}$.
et pour tout réel $x$, $f''(x) = 6x + 12$.
|
Propriétés Lien entre
convexité et $\boldsymbol{f'}$


On se place dans le cas où $f$ est
dérivable sur un
intervalle
$\rm I$.
• $f$ est convexe sur
$\rm I$ si, et seulement si, $\boldsymbol{f'}$ est
croissante sur $\rm
I$.
• $f$ est concave sur
$\rm I$ si, et seulement si, $\boldsymbol{f'}$ est
décroissante sur $\rm
I$.
|
Démontrer que la fonction carré est convexe sur $\mathbb{R}$

Pour tout réel $x$, on a $f(x) = x^2$.
$f$ est dérivable et pour tout réel $x$, $f'(x) = 2x$.
$f'$ est donc strictement croissante sur $\mathbb{R}$ 
$f'$ est une fonction linéaire avec un
coefficient directeur qui vaut 2 donc
strictement positif et donc la fonction $f'$ est
strictement croissante.
Donc la fonction carré est convexe sur $\mathbb{R}$.
|
Propriétés Lien entre
convexité et $\boldsymbol{f''}$


On se place dans le cas où $f$ est deux fois
dérivable
sur un
intervalle
$\rm I$.
• $f$
est convexe sur
$\rm I$ $\Leftrightarrow$ pour tout $x$ de $\rm I$,
$\boldsymbol{f''(x)\geqslant
0}$.
• $f$ est concave sur
$\rm I$ $\Leftrightarrow$ pour tout $x$ de $\rm I$,
$\boldsymbol{f''(x)\leqslant
0}$.
Démonstration
du
théorème en vidéo

Méthode Pour étudier la
convexité d'une fonction

Pour étudier la convexité d'une fonction de
$f$ deux fois
dérivable,
on calcule $f'(x)$ puis $f''(x)$ et ensuite on étudie le
signe de $\boldsymbol{f''(x)}$

Penser à factoriser au maximum
$\boldsymbol{f''(x)}$, car c'est
souvent très
pratique pour étudier son signe.
et on conclut à l'aide de la propriété
précédente

• $f$ est convexe sur
$\rm I$ si, et seulement si, pour tout $x$ de $\rm
I$, $f''\geqslant
0$.
• $f$ est concave sur
$\rm I$ si, et seulement si, pour tout $x$ de $\rm
I$, $f''\leqslant
0$.
|
Étudier la convexité de la fonction $f$ définie sur $\mathbb{R}$ par
$f(x)=x^3+6x^2-3x+1$

$f$ est dérivable sur $\mathbb{R}$

Car $f$ est une fonction
polynôme donc dérivable sur $\mathbb{R}$.
et pour tout réel $x$,
$f'(x)=3x^2+12x-3$.
$f'$ est dérivable sur $\mathbb{R}$ 
Car $f'$ est une fonction
polynôme donc dérivable sur $\mathbb{R}$.
et pour tout réel $x$, $f''(x) = 6x + 12$.
$\begin{equation}
\notag
\begin{array}{|l|ccccc|}
\hline
x&-\infty&&-2&&+\infty\\
\hline
f''(x)&&-&0&+&\\
\hline
\end{array}
\end{equation}$
Donc $f$ est concave sur l'intervalle $]-\infty;-2]$ et
convexe sur l'intervalle $[-2;+\infty[$

Car $f$ est convexe là où $f''(x)\geqslant 0$

C'est à dire sur l'intervalle
$[-2;+\infty[$.
et
est concave là où $f''(x)\leqslant 0$

C'est à dire sur l'intervalle
$]-\infty;-2]$.
|
Définition Point
d'inflexion

Un point d'inflexion est un point où la
courbe traverse sa
tangente. Lorsque la courbe d'une fonction admet
un point d'inflexion,
la fonction change de convexité: elle passe en
ce point de
convexe à concave ou inversement de concave à convexe

Exemple
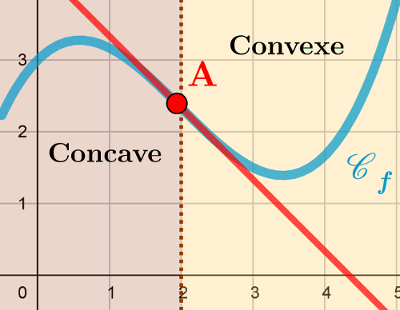
Sur ce graphique, on observe que la courbe de la
fonction $f$ traverse sa tangente en en
$\rm A$.
En $\rm A$, la fonction passe de concave à
convexe.
Autrement dit en $\rm A$, la fonction change de
convexité. $\rm A$ est donc un point
d'inflexion de la
courbe.
Propriété Lien entre point
d'inflexion et dérivée seconde


On se place dans le cas où $f$ est deux fois
dérivable sur un intervalle $\rm I$.
La courbe d'une fonction $f$
admet un point d'inflexion en
$a$ si et seulement si $\boldsymbol{f''}$
s'annule en $a$ en changeant de
signe
Méthode Comment trouver
les points d'inflexion

1) On vérifie que $f$ et dérivable et on calcule
$f'(x)$.
2) On vérifie que $f'$ et dérivable et on calcule
$f''(x)$.
3) On étudie le signe de
$\boldsymbol{f''(x)}$ 
Penser à factoriser
$\boldsymbol{f''}$ au maximum, c'est
très utile pour étudier son signe.
4) Puis on regarde dans le tableau de signe, là où
$\boldsymbol{f''}$ s'annule en changeant de
signe puis on
conclut.
|
Déterminer les points d'inflexion de la courbe de la fonction $f$
définie sur $\mathbb{R}$ par $f(x)=x^3+6x^2-3x+1$

$f$ est dérivable sur $\mathbb{R}$

Car $f$ est une fonction
polynôme donc dérivable sur
$\mathbb{R}$.
et pour tout réel $x$,
$f'(x)=3x^2+12x-3$.
$f'$ est dérivable sur $\mathbb{R}$ 
Car $f'$ est une fonction
polynôme donc dérivable sur
$\mathbb{R}$.
et pour tout réel $x$, $f''(x) = 6x + 12$.
$\begin{equation}
\notag
\begin{array}{|l|ccccc|}
\hline
x&-\infty&&-2&&+\infty\\
\hline
f''(x)&&-&0&+&\\
\hline
\end{array}
\end{equation}$
Donc la courbe de $f$ admet un seul point d'inflexion au
point d'abscisse $-2$

Car le seul endroit où $f''$ s'annule en
changeant de signe est en $-2$.
On peut
retrouver ce résultat graphiquement 
On a tracé en bleu ci-dessous la courbe de $f$
notée $\mathscr{C}_f$:
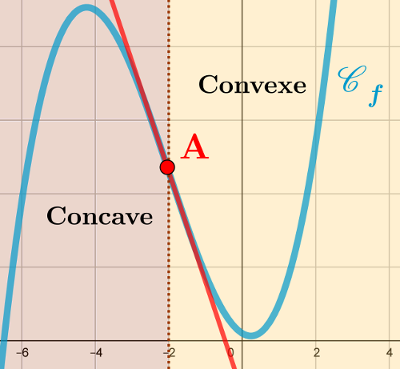
On retrouve graphiquement que la
courbe de la
fonction $f$ traverse sa tangente
(en rouge) au
point $\rm A$ d'abscisse $-2$.
Donc en $\rm A$, la fonction passe de concave à
convexe. Autrement dit en $\rm A$, la fonction
change de convexité. On retrouve donc graphiquement
que $\rm A$ est un
point d'inflexion de la courbe.
|
Méthode Utiliser la
convexité pour obtenir des inégalités


On se place dans le cas où $f$ est
dérivable sur un
intervalle
$\rm I$.
|
À l'aide d'un argument de convexité, montrer que pour tout réel $x$, $x
+ 1 \leqslant \mathrm{e}^x$.

Notons $f$ la fonction exponentielle et $\mathscr{C}_f$ sa
courbe. Donc pour tout réel
$x$, $f(x)=e^x$ et donc $f'(x)=e^x$ et $f''(x)=e^x$.
Or pour tout réel $x$, $e^x\gt 0$ donc $f''(x)\gt 0$ donc
$f$ c'est à dire la fonction exponentielle est convexe sur
$\mathbb{R}$.
Donc la courbe de $f$ est au-dessus de toutes ses tangentes
en particulier celle au point d'abscisse $0$.
Or la tangente à la courbe de $f$ au point d'abscisse $0$ a
pour équation: $y=f'(0)(x-0)+f(0)$$\Leftrightarrow y=e^0
x+e^0$
$\Leftrightarrow y=x+1$. Et comme la courbe de $f$ est au
dessus de cette tangente, on en déduit que pour tout réel
$x$: $x+1\leqslant e^x$

|