probabilité conditionnelle - option maths première

Conseils

Exercice 1:

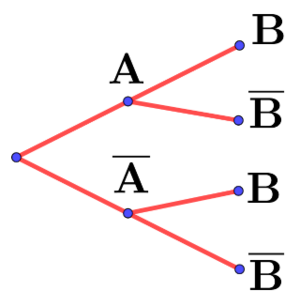
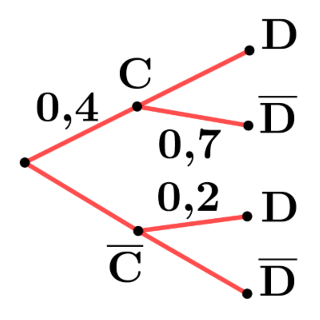
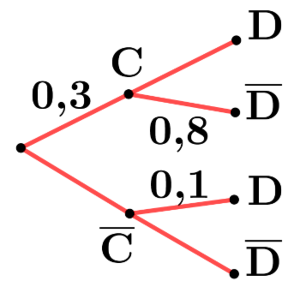
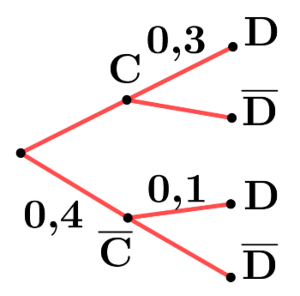
probabilités conditionnelles avec un tableau - première option maths

Voici la répartition des élèves de première d'un lycée selon leur genre et s'ils sont gauchers ou droitiers:

	Gaucher	Droitier	Total
Garçon	$12$	$79$	$91$
Fille	$10$	$75$	$85$
Total	$22$	$154$	$176$

On choisit un élève au hasard. On note les événements :

$\bullet$ F: « L'élève choisit est une fille »
$\bullet$ D: « L'élève choisit est droitier »

Quelle est la probabilité qu'il soit gaucher?
Quelle est la probabilité que ce soit une fille gauchère?
Calculer ${\rm P}_{\rm F}(\rm D)$ puis ${\rm P}_{\rm D}(\rm F)$.

Exercice 2:

arbre de probabilités conditionnelles - option maths première

Compléter l'arbre de probabilités ci-dessous sachant que:
$\bullet~ \rm p(A)=0,4$ $\bullet~ \rm p_A(B)=0,1$ $\bullet~ \rm p_{\overline A}(B)=0,7$

Exercice 3: Arbre et probabilités conditionnelles • Première spécialité mathématiques S - ES - STI

Compléter l'arbre de probabilités ci-dessous:
À l'aide de cet arbre :
1. Donner $\rm p(\overline C)$, $\rm p_{\overline C}(D)$.
2. Déterminer $\rm p(\rm C \cap \overline D)$.

Exercice 4:

arbre de probabilités conditionnelles - option maths première

Compléter l'arbre de probabilités ci-dessous:
À l'aide de cet arbre :
1. Donner $\rm p(\overline C)$, $\rm p_{\overline C}(D)$.
2. Déterminer $\rm p(\rm C \cap D)$.
3. Déterminer ${\rm p}(\rm D)$.

Exercice 5:

arbre de probabilités conditionnelles - inverser le conditionnement - option maths première

Compléter l'arbre de probabilités ci-dessous:
À l'aide de cet arbre :
1. Calculer $\rm p(\rm C \cap D)$ puis ${\rm p}(\rm D)$.
2. En déduire $\rm p_{D}(\rm C)$.

Exercice 6:

arbre de probabilités conditionnelles - inverser le conditionnement - option maths première

On considère l'arbre de probabilité :

On sait que $\rm P(S)=0,34$

Déterminer $\rm P(A)$.
Déterminer $\rm P_{S}(A)$.

Exercice 7: probabilités conditionnelles - arbre pondéré - Première spécialité maths S - ES - STI

Un sac contient dix jetons dont sept sont blancs. Samuel prend un jeton au hasard qu'il ne remet pas dans le sac. Puis Rose prend au hasard un jeton dans le sac.
On note S l'événement « le jeton de Samuel est blanc » et R l'événement « le jeton de Rose est blanc ».

Réaliser un arbre pondéré correspondant à la situation.
Déterminer la probabilité que Samuel et Rose prennent chacun un jeton blanc.

Exercice 8: probabilités conditionnelles - - arbre pondéré - Première spécialité maths S - ES - STI

80% des clients d'une station de carburant utilisent des pompes en libre service et 90% d'entre eux prennent du gazole. Parmi les clients qui utilisent les autres pompes, 60% prennent du gazole.
On choisit un client au hasard. On note L l'événement « le client utilise une pompe en libre service » et G l'événement « le client achète du gazole ».

Réaliser un arbre pondéré correspondant à la situation.
Déterminer la probabilité que le client ne se serve pas à une pompe en libre service et qu'il ne prenne pas du gazole.

Exercice 9:

arbre de probabilités conditionnelles - Tennis - option maths première

Un joueur de tennis réussit sa première balle de service avec une probabilité de $0,7$. S'il ne réussit pas sa première balle de service, il réussit sa seconde balle de service avec une probabilité de $0,9$. On note les événements:
$\bullet$ $\rm R_1$ : « Il réussit sa première balle de service. »
$\bullet$ $\rm R_2$ : « Il réussit sa deuxième balle de service. »

Représenter la situation par un arbre de probabilités.
Quelle est la probabilité qu'il commette une double faute?

Exercice 10:

arbre de probabilités conditionnelles - Liban juin 2004 - maths première

Le personnel d'un hôpital est réparti en trois catégories : M (médecins), S (soignants non médecins) et AT (personnel administratif ou technique). On note H : la personne est un homme.
• 12% sont des médecins et 71% des soignants.
• 67% des médecins sont des hommes et 92% des soignants sont des femmes.
On interroge au hasard un membre du personnel

Construire un arbre pondéré correspondant à la situation et compléter l'arbre avec les informations fournies dans l'énoncé.
Quelle est la probabilité d'interroger une femme soignante ? une femme médecin ?
On sait que 80% du personnel est féminin. En déduire la probabilité d'interroger une femme sachant que la personne interrogée fait partie du personnel AT.

Exercice 11:

arbre de probabilités conditionnelles - Liban juin 2004 - maths première

Un lot de cent dés contient vingt dés truqués. Pour un tel dé, la probabilité d'apparition du 6 est égale à $\dfrac 12$. Les autres dés sont équilibrés. On note les événements :
• T : « le dé est truqué »
• S : « on obtient 6. »

Construire un arbre pondéré correspondant à la situation.
On prend au hasard un dé. Quelle est la probabilité d'obtenir 6 ?
On a pris au hasard un dé, que l'on a lancé et on a obtenu 6. Quelle est la probabilité que ce dé soit truqué ?

Exercice 12:

probabilités conditionnelles avec un tableau - première option maths

On souhaite tester l'efficacité d'un nouveau médicament destiné à lutter contre l'excès de cholestérol. Des essais sont faits sur un échantillon de patients présentant un excès de cholestérol dans le sang. Certains patients reçoivent le médicament tandis que d'autres reçoivent un placebo (comprimé sans principe actif). La répartition est indiquée dans le tableau ci-dessous:

	Placebo	Médicament
Guéri	$12$	$119$
Non guéri	$48$	$21$

On choisit un patient au hasard et on note les événements:

$\bullet$ M: « Le patient a reçu le médicament. »
$\bullet$ G: « Le patient est guéri. »

Déterminer les probabilités suivantes:

$ \color{red}{\textbf{a. }} \rm p(M)$ $\color{red}{\textbf{b. }} \rm p(M\cap \overline{G})$ $\color{red}{\textbf{c. }} \rm p_{M}(G)$ $\color{red}{\textbf{d. }} \rm p_{\overline G}(M)$

Tous les niveaux couverts

Collège

Lycée

Supérieur

Manuels scolaires pour lesquels j'ai réalisé les vidéos

Jaicompris.com — dans la presse et les médias

Prêt à transformer ton apprentissage ?

Rejoins des milliers d'élèves qui ont déjà amélioré leurs résultats en mathématiques

Ce site ne convient pas aux enfants de moins de 36 mois, sauf s'ils insistent vraiment.
Ne pas dépasser la dose prescrite.
Posologie: 1 fois/jour la semaine avant le contrôle.
L'efficacité du traitement dépend d'une prise régulière.
Effet secondaire: Peut procurer du plaisir surtout en cas de réussite !
En cas de persistance des difficultés, arrêter le traitement pendant une nuit, puis reprendre le lendemain.

Site jaicompris 100% gratuit avec accès illimité aux vidéos et exercices

Académie de Poitiers – page mathématiques

Icône humoristique : satisfait ou remboursé, mais gratuit

🎥 10 ans de collaboration avec les éditions Nathan

🎬 Ma dernière vidéo

Probabilités conditionnelles

probabilités conditionnelles avec un tableau - première option maths

arbre de probabilités conditionnelles - option maths première

Exercice 3: Arbre et probabilités conditionnelles • Première spécialité mathématiques S - ES - STI

arbre de probabilités conditionnelles - option maths première

arbre de probabilités conditionnelles - inverser le conditionnement - option maths première

arbre de probabilités conditionnelles - inverser le conditionnement - option maths première

Exercice 7: probabilités conditionnelles - arbre pondéré - Première spécialité maths S - ES - STI

Exercice 8: probabilités conditionnelles - - arbre pondéré - Première spécialité maths S - ES - STI

arbre de probabilités conditionnelles - Tennis - option maths première

arbre de probabilités conditionnelles - Liban juin 2004 - maths première

arbre de probabilités conditionnelles - Liban juin 2004 - maths première

probabilités conditionnelles avec un tableau - première option maths

Tous les niveaux couverts

Lycée

Supérieur

Manuels scolaires pour lesquels j'ai réalisé les vidéos

Jaicompris.com — dans la presse et les médias

Prêt à transformer ton apprentissage ?