Exercice
1: Comprendre le lien entre les nombres complexes et les points et vecteurs
Dans le plan complexe, $\rm A$, $\rm B$ et $\rm C$ sont les points d'affixes :
$z_{\rm A} = 5 + 3i$, $z_{\rm B} = 8 + i$ et $z_{\rm C} = 1 -3i$.
Déterminer l'affixe du point $\rm D$ tel que $\rm ABCD$ soit un parallélogramme.
Exercice
2: Comprendre le lien entre les nombres complexes et les points et vecteurs
1) Lire les affixes $z_A$, $z_B$ et $z_C$ des points A,B et C.
2) Déterminer l'affixe du vecteur $\overrightarrow {AB}$ graphiquement
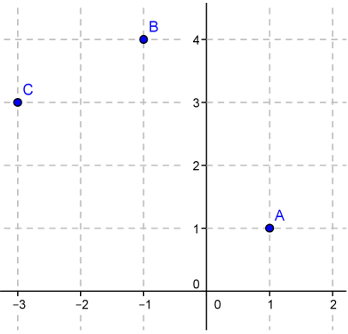
puis à l'aide des affixes.
3) Déterminer l'affixe de I milieu de [AC] graphiquement
puis à l'aide des affixes.
4) Déterminer de deux façons différentes l'affixe du point D
tel que ABCD soit un parallélogramme.
Exercice
3: Nombre complexe et vecteur - affixe d'un point défini vectoriellement
Soit A, B et C d'affixes respectives $z_A=-3+2i$ $z_B=1-2i$ $z_C=-1+6i$.
On considère le point M tel que $3\overrightarrow{MB}-\overrightarrow{MA}=\overrightarrow{AC}$.
1) Déterminer l'affixe $z_M$ du point M et en déduire ses coordonnées.
2) Faire une figure et placer les points A, B, C et M.
3) Soit D le symétrique de A par rapport à B. Déterminer l'affixe $z_D$ du point D.
4) Les points M, D et C sont-ils alignés? Justifier.
Exercice
4: Nombre complexe et milieu, centre de gravité, triangle
Soit A, B, C d'affixes respectives $z_A$, $z_B$ et $z_C$.
1) Soit I: le milieu du segment [AB]. On note $z_I$ l'affixe de I.
a) Rappeler la définition vectorielle de I.
b) En déduire $z_I$ en fonction de $z_A$ et $z_B$.
2) Soit G le centre de gravité du triangle A, B, C. On note $z_G$ l'affixe de G.
On rappelle que G vérifie
$\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow{0}$.
Déterminer $z_G$ en fonction de $z_A$, $z_B$ et $z_C$.
3) On donne $z_A=3+2i$, $z_B=-2+5i$ et $z_C=-5-4i$.
a) Déterminer l'affixe de J, milieu de [BC].
b) Déterminer l'affixe de G, centre de gravité du triangle ABC.
c) Les points J, G et A sont-ils alignés? Justifier.
d) Cela était-il prévisible? Justifier.
Exercice
5: Affixe d'un vecteur - Démonstration de cours - ROC
On rappelle que l'affixe du vecteur $\overrightarrow{OM}$ est égale à l'affixe du point M. Autrement dit
$z_{\overrightarrow {OM}}=z_{M}$.
Soit A et B deux points d'affixes respectives $z_A$ et $z_B$.
1) Décomposer le vecteur $\overrightarrow{AB}$ en fonction des vecteurs $\overrightarrow{OA}$ et
$\overrightarrow{OB}$.
2) En déduire l'affixe du vecteur $\overrightarrow{AB}$ en fonction de $z_A$ et $z_B$.
Exercice
6: Un classique - Complexe - Ensemble de points - cercle
Dans le plan complexe, déterminer et construire l'ensemble des points M d'affixe $z$ tels que $2z\overline{z}=3(z+\overline{z})$
Exercice
7: D'après sujet de Bac
Exercice 6: D'après sujet de Bac
Le plan complexe est muni d'un repère orthonormé direct $(O; \overrightarrow{u} ; \overrightarrow{v}
)$.
À tout point $M$ d'affixe $z$, on associe le point $M'$ d'affixe $z'=z^2+4z+3$.
Déterminer l'ensemble E des points $M$ d'affixe $z = x +iy$ où $x$ et $y$ sont réels,
tels que le
point $M'$ soit sur l'axe des réels. Puis représenter l'ensemble E.
Exercice
8: Condition pour qu'un complexe soit réel - imaginaire pur - Ensemble de
points
Le plan complexe est muni d'un repère orthonormé direct $(O; \overrightarrow{u} ; \overrightarrow{v}
)$.
Soit $z$ un nombre complexe différent de $i$.
On note \[z'=\frac{z+i}{z-i}\]. On appelle X et Y respectivement la partie
réelle et imaginaire de $z'$.
1) On pose $z=x+iy$ où $x$ et $y$ sont réels. Déterminer X et Y en fonction de $x$ et $y$.
2) Déterminer l'ensemble $\mathscr E_1$ des points M d'affixe $z$ tels que $z'$ est réel.
3) Déterminer l'ensemble $\mathscr E_2$ des points M d'affixe $z$ tels que $z'$ est imaginaire pur.
Corrigé en vidéo
Exercice
9:
Le plan complexe est muni d'un repère orthonormé direct $(O; \overrightarrow{u} ; \overrightarrow{v} )$.
À tout point $M$ d'affixe $z$ différente de $3i$, on associe le point $M'$ d'affixe \[z'=\frac{z-2}{iz+3}\].
On appelle X et Y respectivement la partie réelle et imaginaire de $z'$.
1) On pose $z=x+iy$ où $x$ et $y$ sont réels. Déterminer X et Y en fonction de $x$ et $y$.
2) Déterminer l'ensemble $\mathscr E_1$ des points M d'affixe $z$ tels que $z'$ soit réel.
3) Déterminer l'ensemble $\mathscr E_2$ des points M d'affixe $z$ tels que $z'$ soit imaginaire pur.
Corrigé en vidéo
Exercice
10: Nombre complexe et alignement
On considère la suite de nombres complexes $(z_n)$ définie par $z_0=100$ et pour tout entier naturel $n$,
$z_{n+1}=\frac i3 z_n$.
Le plan est muni d'un repère orthonormé direct (O;$\vec u$;$\vec v$).
Pour tout entier naturel $n$, on note ${\rm M}_n$ le point d'affixe $z_n$.
Démontrer que pour tout entier naturel $n$, les points ${\rm O}$, ${\rm M}_n$ et ${\rm M}_{n+2}$ sont
alignés.
Web
