QCM en ligne!

1: Exercice en ligne: pour s'entrainer au calcul de
module de nombre complexe
QCM en ligne pour s'entrainer !

2: Module graphiquement et par le calcul -
$|z_B-z_A|$ - module et triangle équilatéral
On considère la figure suivante:
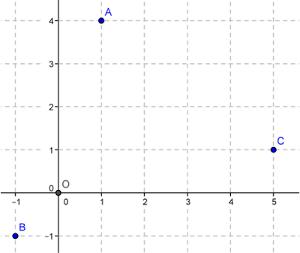
1) À l'aide d'un compas, déterminer une valeur approchée
des longueurs OA, OB, OC, AB, AC et BC.
2) Lire les affixes $z_A$, $z_B$, $z_C$ des points A, B et C.
3) Déterminer $|z_A|$, $|z_B|$, $|z_C|$. Est-ce cohérent?
4) Déterminer $|z_C-z_A|$, $|z_B-z_A|$ et $|z_B-z_C|$. Est-ce cohérent?
5) Le triangle ABC est-il rectangle, isocèle ou équilatéral?


Corrigé en vidéo!
3: Nathan Hyperbole Option Maths - Expertes Exerice 42 Chapitre 2
Calculer le module de chaque nombre complexe suivant:
$z_1=3+3i$ $z_2=-\sqrt{3}+i$ $z_3=-\dfrac 25i$ $z_4=-6+6i\sqrt{3}$


Corrigé en vidéo!
4: Nathan Hyperbole Option Maths Expertes - Exerice 47 Chapitre 2
Calculer le module de chaque nombre complexe suivant:
$z_1=(5+2i)\left(\sqrt{ 3}+i\sqrt{6}\right)$ $z_2= \left(\dfrac{\sqrt{3}-i}{4i}\right)^{\!\! 3}$


Corrigé en vidéo!
5: Calculer un module d'un nombre complexe
Déterminer le module de $z$ dans chacun des cas suivants:
\[z=2\]
\[z=-3\]
\[z=4i\]
\[z=\sqrt{3}+3i\]
\[z=\frac 2i\]
\[z=\cos \frac {\pi}3-i\sin \frac {\pi}3\]


6: Module d'un nombre complexe - Démonstration de cours - ROC
Démontrer que pour tout nombre complexe $z$, $|-z|=|\overline z|=|z|$.


7: Comment utiliser les Propriétés des modules pour calculer un module
rapidement
Soit $z_1=\sqrt 2 +i\sqrt 6$ et $z_2=2+2i$.
Déterminer les modules de $z_1$, $z_2$, $-\sqrt 2 -i\sqrt 6$, $2-2i$ et de \[\frac{-\sqrt 2 -i\sqrt 6}{(2-2i)^2}\]


Corrigé en vidéo
8: Module d'un produit, d'un quotient, d'une somme
1) Déterminer le module de $z_1=1-i\sqrt 3$ et $z_2=-1+i$.
2) Déterminer le module des nombres suivants, en utilisant si possible la question 1)
\[\frac{-1+i\sqrt 3}{-1-i}\]
\[-\frac12(-1+i\sqrt 3)\]
\[\frac{(1-i\sqrt 3)^2}{(1-i)^3}\]
\[\frac 14-\frac 14i\]
\[z_1+z_2\]


Corrigé en vidéo!
9: Interpréter un module en terme de longueur - lien avec cercle et médiatrice
Déterminer l'ensemble des points M d'affixe $z$ dans chacun des cas suivants:
\[a)~|z-3|=4\]
\[b)~|z+1-i|=3\]
\[c)~|z+2|=|z-2+3i|\]
\[d)~|4-z|=|\overline z-1+2i|\].


Corrigé en vidéo!
10: D'après le sujet Bac Centres étrangers 2015 exercice 2
Dans le plan muni d'un repère orthonormé, construire l'ensemble $\mathcal{S}$ des points M
dont l'affixe $z$ vérifie les deux conditions: $\left\{
\begin{array}{l}
|z-i|=|z+1| \\
|z+3-2i|\le 2
\end{array}
\right.$


Corrigé en vidéo!
11: lieu des points M d'affixe z tels que |z-a|=|z-b| par deux méthodes
Le plan complexe est muni d'un repère orthonormé direct $(O; \overrightarrow{u} ; \overrightarrow{v} )$.
On note $\Gamma$ l'ensemble des points M dont l'affixe $z$ vérifie $|z-2-3i|=|z-4+i|$.
1) Justifier que le point $C(1;0)$ appartient à $\Gamma$.
2) Déterminer l'ensemble $\Gamma$ en posant $z=x+iy$ et le représenter.
3) Refaire la question 2) par une autre méthode.


12: Nombre complexe et géométrie - Triangle - point sur un même cercle
On considère les points A, B, C d'affixes respectives $z_A=-1-5i$, $z_B=7+i$ et $z_C=8-2i$.
1) Déterminer la nature du triangle ABC.
2) En déduire que A, B et C sont sur un même cercle. On note I le centre de ce cercle.
Déterminer l'affixe de I et le rayon de ce cercle.
3) Le point D(0;2) est-il également sur ce cercle? Justifier.


13: Module d'un nombre complexe - point sur un même cercle
Le plan complexe est muni d'un repère orthonormé direct $(O; \overrightarrow{u} ; \overrightarrow{v} )$.
À tout point $M$ d'affixe $z$ différente de $3i$, on associe le point $M'$ d'affixe \[z'=\frac{z-2}{iz+3}\].
Déterminer l'ensemble $\mathscr E$ des points M d'affixe $z$ tels que M' soit sur le cercle de centre O et
de rayon 1.


14:
On considère les points A, B, C d'affixes respectives $z_A=\sqrt 3+2i$, $z_B=-\overline{z}_A$ et
$z_C=-i$.
1) On a placé le point A sur la figure ci-contre:
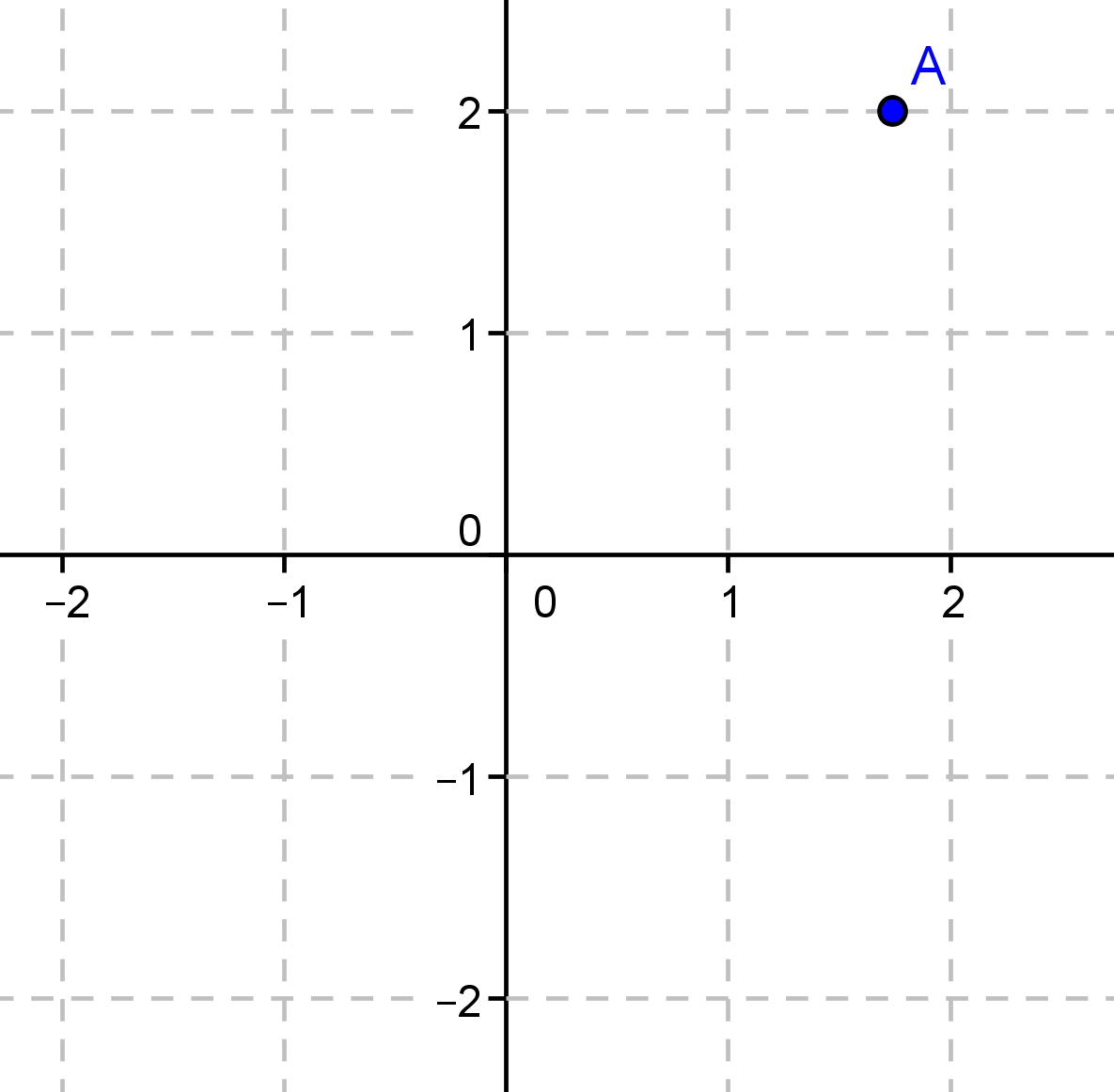
Placer les points B et C.
2) Démontrer que le triangle ABC est équilatéral.
3) Soit G, le centre de gravité du triangle ABC.
a) Placer le point G sur la figure
en faisant apparaitre les traits de construction.
b) Rappeler la définition vectorielle de G.
c) Déterminer $z_G$, l'affixe de G.
4) Soit I le milieu du segment [AG].
Déterminer $z_I$, l'affixe de I. Placer le point I sur la figure.
5) Soit J, le point tel que GIJC soit un parallélogramme. Déterminer $z_J$, l'affixe de J.
6) Démontrer que les droites (GJ) et (CJ) sont perpendiculaires.
7) En déduire que J est sur un cercle que l'on précisera. Placer J sur la figure.


Corrigé en vidéo!
15: Suite de nombres complexes - Suite de nombre complexe - Sujet Bac S Antilles
Guyane 2015
Le plan complexe est muni d'un repère orthonormé direct $(O; \overrightarrow{u} ; \overrightarrow{v} )$.
On a placé un point $M$ d'affixe $z$ sur la figure ci-contre:

Soit $M'$ le point d'affixe
\[z'=\frac 12\left(\frac {z+|z|}2
\right)\].
1) Construire le point $M'$ sur la figure en laissant les traits de construction.
2) On définit la suite de nombres complexes ($z_n$) de premier terme $z_0$
appartenant à $\mathbb{C}$ et pour tout entier naturel $n$:
\[z_{n+1}=\frac{z_n+|z_n|}4\].
a) Que peut-on dire du comportement à l'infini de la suite ($|z_n|$) quand $z_0$
est un réel négatif?
b) Que peut-on dire du comportement à l'infini de la suite ($|z_n|$) quand $z_0$
est un réel positif?
c) On suppose désormais que $z_0$ n'est pas un nombre réel.
Que peut-on dire du comportement à l'infini de la suite
($|z_n|$)? Justifier.


Corrigé en vidéo!
16: Problème ouvert - Module
Quels sont les nombres complexes $z$ tels $z$, \[\frac{1}{z}\] et $1-z$
aient même module?


Corrigé en vidéo!
17: Problème ouvert - Suite de nombres complexes et disque
On considère la suite de nombres complexes $(z_n)$ définie par
$z_0=100$ et pour tout entier
naturel $n$, $z_{n+1}=\frac i3 z_n$.
Le plan est muni d'un repère orthonormé direct (O;$\vec u$;$\vec v$). Pour tout entier naturel $n$, on
note ${\rm M}_n$ le point d'affixe $z_n$. On rappelle qu'un disque de centre A et de rayon $r$, où $r$
est un réel positif, est l'ensemble des points M du plan tels que ${\rm AM}\le r$.
Démontrer qu'à partir d'un certain rang, tous les points ${\rm M_n}$ appartiennent au disque de centre
${\rm O}$ et de rayon $1$.


Corrigé en vidéo!
18: Nombres complexes et triangle équilatéral
Le plan complexe est muni d'un repère orthonormé ${(\rm O};\vec u;\vec v)$.
Gaspard affirme que l'équation $z^3-3z^2+3z=0$ admet trois solutions dans l'ensemble des nombres
complexes $\mathbb{C}$, qui sont les affixes de trois points formant un triangle équilatéral. Gaspard
a-t-il raison? Justifier.


Corrigé en vidéo!
19: Nombres complexes, équation et points sur un cercle
On considère dans $\mathbb{C}$ l'équation $(4z^2-20z+37)(2z-7+2i)=0$.
Nasser affirme que les solutions de cette équation sont les affixes de points appartenant à un même
cercle de centre $\rm P$ d'affixe 2. Nasser a-t-il raison? Justifier.


20: Problème ouvert
On rappelle la régle du produit nul: $x.y=0 \Rightarrow x=0$ ou $y=0$
Cette règle qui est vraie avec des nombres réels, est-elle encore vraie avec des nombres complexes?


Corrigé en vidéo!
21: Triplets pythagoriciens et Module d'un nombre complexe
On s'intéresse aux triplets d'entiers naturels non nuls $(x, y, z)$ tels que $x^2 + y^2 = z^2$.
Ces triplets sont nommés « triplets pythagoriciens » en référence aux triangles rectangles dont ils
mesurent les côtés.
- Le but de cette question est de trouver un triplet pythagoricien à l'aide des nombres
complexes.
On considère le nombre complexe $z=3+2i$.
a) Déterminer $z^2$ sous forme algébrique.
b) Déterminer $|z^2|$.
c) En déduire un triplet pythagoricien.
- Généraliser la méthode de la question 1. pour trouver une infinité de triplets pythagoriciens.







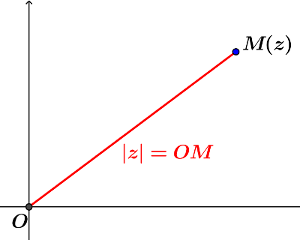


















 1) À l'aide d'un compas, déterminer une valeur approchée
1) À l'aide d'un compas, déterminer une valeur approchée






 6: Module d'un nombre complexe - Démonstration de cours - ROC
6: Module d'un nombre complexe - Démonstration de cours - ROC
 7: Comment utiliser les Propriétés des modules pour calculer un module
rapidement
7: Comment utiliser les Propriétés des modules pour calculer un module
rapidement










 13: Module d'un nombre complexe - point sur un même cercle
13: Module d'un nombre complexe - point sur un même cercle

 Placer les points B et C.
Placer les points B et C.

 Soit $M'$ le point d'affixe \[z'=\frac 12\left(\frac {z+|z|}2
\right)\].
Soit $M'$ le point d'affixe \[z'=\frac 12\left(\frac {z+|z|}2
\right)\].













