j'ai compris mes maths
jaicompris.com
Cours et exercices corrigés en vidéo
Pour rechercher un exercice ou un cours sur jaicompris.com :
Quatrième

Résoudre une équation du premier degré

Trustpilot
Trustpilot
Conseils
Résoudre une équation du premier degré
Cours

savoir résoudre une équation du premier degré (en 3 min !)

Équation du premier degré
A savoir
Méthode pour résoudre
Exemple Résoudre $2-4x=x-8$

Exercice type

résoudre une équation du 1er degré (en 3 min !) ♦ Niveau 1


Exercice type

résoudre une équation du 1er degré (en 5 min !) ♦ Niveau 2


Exercice type

résoudre une équation du 1er degré (en 4 min !) ♦ Niveau 3


Exercice type

savoir si un nombre est solution d'une équation (en 4 min!)


Conseil important

pourquoi :"Je fais passer de l'autre côté" amène à faire des erreurs


Cours

Qu'est-ce qu'une équation, une inconnue, une solution

, expliqué en vidéo
Équation, inconnue
Solution
Résoudre
Cours

Les 4 règles de base pour résoudre une équation

, expliquées en vidéo
Principe général
•

Règle avec l'addition

•

Règle avec la soustraction

•

Règle avec la multiplication

•

Règle avec la division

Ancienne version du cours

Equation du premier degré

, expliquées en vidéo
Tape ton expression + clique sur X=

Exercice 1: Résoudre une équation du premier degré - Cinquième Quatrième Troisième collège

Résoudre chaque équation:
$\color{red}{\textbf{a. }} 5x+3=28$ $\color{red}{\textbf{b. }} 3(x+4)=9$ $\color{red}{\textbf{c. }} 2x+3=11$ $\color{red}{\textbf{d. }} 5-3x=17$ $\color{red}{\textbf{e. }} 5-3x=14$

Exercice 2: Savoir si un nombre est solution d'une équation- Cinquième Quatrième Troisième collège

$2$ est-il solution de l'équation:
  1. $10-3x=4$
  2. $3x-1=5x-3$

Exercice 3: Résoudre une équation du premier degré - Cinquième Quatrième Troisième collège

Résoudre chaque équation:
$\color{red}{\textbf{a. }} x-8=0$ $\color{red}{\textbf{b. }} x+8=0$ $\color{red}{\textbf{c. }} 8x=0$ $\color{red}{\textbf{d. }} \dfrac x8=0$

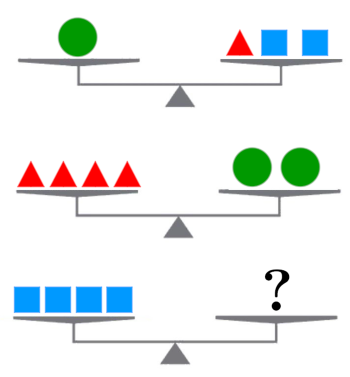
Exercice 4: équilibrer une balance - énigme mathématiques - équation - collège - cinquième quatrième

Donner deux réponses possibles

Exercice 5: Résoudre une équation du premier degré - Cinquième Quatrième Troisième collège

Résoudre chaque équation:
$\color{red}{\textbf{a. }} x-4=5$ $\color{red}{\textbf{b. }} x+4=7$ $\color{red}{\textbf{c. }} 4x=6$ $\color{red}{\textbf{d. }} \dfrac x4=5$

Exercice 6: Résoudre une équation du premier degré - Cinquième Quatrième Troisième collège

Résoudre chaque équation:
$\color{red}{\textbf{a. }} 2x=6$ $\color{red}{\textbf{b. }} 7y-5=6y$ $\color{red}{\textbf{c. }} -4a=0$ $\color{red}{\textbf{d. }} 9-4b=-15$

Exercice 7: Résoudre une équation du premier degré - Cinquième Quatrième Troisième collège

Résoudre chaque équation:
$\color{red}{\textbf{a. }} 4x=20$ $\color{red}{\textbf{b. }} x+4=7$ $\color{red}{\textbf{c. }} -2x=6$ $\color{red}{\textbf{d. }} \dfrac x4=3$

Exercice 8: Résoudre une équation du premier degré - Cinquième Quatrième Troisième collège

Résoudre chaque équation:
$\color{red}{\textbf{a. }} 5x-7=2x-1$ $\color{red}{\textbf{b. }} 3x+1=4-2x$

Exercice 9: Résoudre une équation du premier degré - Cinquième Quatrième Troisième collège

Résoudre l'équation: $5x-6=-x+3$

Exercice 10: Résoudre une équation du premier degré - mathématiques - seconde

Résoudre dans $\mathbb{R}$ les équations suivantes:
$\color{red}{\textbf{a. }} 5(x+4)=7x+6$ $\color{red}{\textbf{b. }} 4(2-x)=3(x+2)$

Exercice 11: Résoudre une équation du premier degré - Cinquième Quatrième Troisième collège

Résoudre chaque équation:
$\color{red}{\textbf{a. }} \dfrac 92 x-1=2+3x$ $\color{red}{\textbf{b. }} 2x-\dfrac 13=1$

Exercice 12: Résoudre une équation du premier degré avec fraction quotient - Cinquième Quatrième Troisième collège

Résoudre chaque équation:
$\color{red}{\textbf{a. }} \dfrac x3 +4=2x-1$ $\color{red}{\textbf{b. }} x-\dfrac 12=\dfrac x3 +1$

Exercice 13: Résoudre une équation du premier degré - mathématiques - Cinquième Quatrième Troisième collège

Résoudre les équations suivantes:
$\color{red}{\textbf{a. }} \dfrac x4=\dfrac x3-\dfrac 12$ $\color{red}{\textbf{b. }} \dfrac {7x}6-\dfrac23=\dfrac{5x}{2}$

Exercice 14: Savoir si un nombre est solution d'une équation - Cinquième Quatrième Troisième collège

Dire si -2 est solution des équations suivantes:
$\color{red}{\textbf{a. }} x+2=0$ $\color{red}{\textbf{b. }} -t-2=0$ $\color{red}{\textbf{c. }} -t^2+t+6=0$

Exercice 15: Savoir si un nombre est solution d'une équation

Trouver mentalement une solution de chacune des équations suivantes:
$\color{red}{\textbf{a. }} 2y+3=11$ $\color{red}{\textbf{b. }} 4a^2=3a$ $\color{red}{\textbf{c. }} (3-b)^2=0$

Exercice 16: Résoudre une équation du premier degré - Cinquième Quatrième Troisième collège

Résoudre chaque équation:
$\color{red}{\textbf{a. }} \dfrac 25x=-4$ $\color{red}{\textbf{b. }} -\dfrac 25+x=-4$

Exercice 17: Résoudre une équation du premier degré - Cinquième Quatrième Troisième collège

Résoudre les équations suivantes:
$\color{red}{\textbf{a. }} 4x-1=19$ $\color{red}{\textbf{b. }} -4t=0$ $\color{red}{\textbf{c. }} \dfrac x3 +1=5$

Exercice 18: Résoudre une équation du premier degré - Cinquième Quatrième Troisième collège

Résoudre les équations suivantes:
$\color{red}{\textbf{a. }} (7+4x)-(x-6)=0$ $\color{red}{\textbf{b. }} 8(1-x)-3(4-2x)=0$

Exercice 19: Résoudre une équation du premier degré - mathématiques Cinquième Quatrième Troisième collège

Résoudre les équations suivantes:
$\color{red}{\textbf{a. }} -t-6=9+4t$ $\color{red}{\textbf{b. }} \dfrac x7=3$ $\color{red}{\textbf{c. }} -4y=y$ $\color{red}{\textbf{d. }} 2,5a+3=5a+7$

Exercice 20: Résoudre une équation du premier degré avec fraction - mathématiques Cinquième Quatrième Troisième collège

Résoudre les équations suivantes:
$\color{red}{\textbf{a. }} 4(2y+3)-12=-y+6(2y+1)$ $\color{red}{\textbf{b. }} 3t-\dfrac 23=1$ $\color{red}{\textbf{c. }} \dfrac x5=\dfrac 54$ $\color{red}{\textbf{d. }} \dfrac{4z}{7}=-\dfrac 4{21}$

Exercice 21: Résoudre une équation du premier degré avec fraction - Mathématiques - Cinquième Quatrième Troisième collège

Résoudre les équations suivantes:
$\color{red}{\textbf{a. }} \dfrac x4+5=\dfrac {4x}2-1$ $\color{red}{\textbf{b. }} \dfrac 85t-\dfrac 23=t$ $\color{red}{\textbf{c. }} \dfrac 19y+\dfrac 13=1-y$

Exercice 22: Résoudre une équation du premier degré - Mathématiques - Cinquième Quatrième Troisième collège

Voici quatre équations. Trouver celles qui ont la même solution:
$\color{red}{\textbf{ ① }} 4(x+2)=x-1$ $\color{red}{\textbf{② }} 5y+1=3(y-1)-2$ $\color{red}{\textbf{③ }} 3n-1=2(n+1)$ $\color{red}{\textbf{④ }} 4(a+1)-5=6a+5$

Exercice 23: Résoudre des équations en ligne - exercice en ligne pour s'entrainer

Score:0

Résoudre:
$10x-2=3$




Trustpilot
Trustpilot