Argument d'un nombre complexe - Forme exponentielle

Argument d'un nombre complexe

♦ Cours sur l'argument en vidéo

Soit z, non nul, l'affixe de M. Un argument de z noté arg(z)=

$\arg(z)$ est égal à une mesure de l'angle $\left(\overrightarrow{u};\overrightarrow{\mathrm{OM}}\right)$.

On ne peut parler d'argument que si
$z$ est non nul.

Si $z=0$,
ça n'a pas de sens de parler d'argument!

Un argument est défini à 2π près.

Si $\alpha$ est un argument de $z$,
$\alpha+2\pi$ est un autre argument de $z$

C'est pour cela
qu'on ne dit pas l'argument
Mais un argument.
Pour trouver un argument de z

1°) On calcule le module de $z$, noté |z|
2°) On appelle α un argument de z
On calcule cos(α) =
a / |z|
et sin(α) =
b / |z|

3°) On trouve α
à l'aide du cercle trigonométrique
\[\arg(\overline z)=\]

$\arg(\overline z)=-\arg(z)$ $[2\pi]$

• Cette propriété est vraie à 2$\pi$ près!
• Ne pas oublier que $z$ est un complexe non nul.

\[\arg(-z)=\]

$\arg(-z)=\arg(z)+\pi$ $\left[2\pi\right]$

• Cette propriété est vraie à 2$\pi$ près!
• Ne pas oublier que $z$ est un complexe non nul.

arg(réel)

Si $r\gt 0$ $\arg(r)=0$

car $\arg(r)=\left(\overrightarrow{u};\overrightarrow{\mathrm{OM}}\right)=0$

Si $r\lt 0$ , $\arg(r)=\pi$

car $\arg(r)=\left(\overrightarrow{u};\overrightarrow{\mathrm{OM}}\right)=\pi$

\[\arg(i)=\]

\[\arg(i)=\frac{\pi}2\]

car \[\arg(i)=\left(\overrightarrow{u};\overrightarrow{\mathrm{OM}}\right)=\frac{\pi}2\]
$z_1=z_2$

$z_1=z_2$
$\Updownarrow$
$z_1$ et $z_2$ ont même partie réelle et même partie imaginaire
$\Updownarrow$
$z_1$ et $z_2$ ont même module et même argument à $2\pi$ près

$z_1$ et $z_2$ sont 2 complexes non nuls.

Forme trigonométrique

♦ Cours sur la forme trigonométrique d'un nombre complexe, en vidéo

Soit z un complexe de module r et d'argument $\alpha$ alors

$z=r(\cos\alpha + i \sin\alpha)$

On dit qu'on a écrit $z$ sous forme trigonométrique.
Pour écrire $z$, non nul, sous forme trigonométrique

1) Déterminer le module de $z$

Si $z=a+ib$ avec $a$ et $b$ réels:
\[|z|=\sqrt{a^2+b^2}\]

2) Puis un argument de $z$

Si $z=a+ib$ avec $a$ et $b$ réels:
1) On note $\alpha$ un argument de $z$.
2) Puis on utilise les formules:
\[\cos\alpha=\frac a{|z|}\] et \[\sin\alpha=\frac b{|z|}\]
3) On trouve $\alpha$ à l'aide du cercle trigo.

3) Puis remplacer dans la formule $z=r(\cos\alpha + i \sin\alpha)$
$r$ par le module de $z$ et $\alpha$ par un argument de $z$.
Si $z=r(\cos\alpha + i \sin\alpha)$ alors

Si $z=r(\cos\alpha + i \sin\alpha)$ avec r strictement positif et $\alpha$ réel
alors
le module de $z$ vaut $r$ et un argument de $z$ vaut $\alpha$

Si $r$ n'est pas positif, on ne peut pas conclure directement.
Voir les exercices.

Notation exponentielle

♦ Cours sur la notation exponentielle d'un nombre complexe, en vidéo

L'expression cosα + isinα=

$\cos\alpha + i\sin\alpha$ est noté $e^{i\alpha}$ où $\alpha$ est un nombre réel

Autrement dit: $e^{i\alpha}=\cos\alpha + i\sin\alpha$

$\left|e^{i\alpha}\right|=$

$\left|e^{i\alpha}\right|=1$

où $\alpha$ est un nombre réel.

et arg(e^iα) =

un argument de $e^{i\alpha}$ est $\alpha$

où $\alpha$ est un nombre réel.
si $z$ est un nombre complexe de module r et d'argument α alors

$z=re^{i\alpha}$
On dit qu'on a écrit $z$ sous
forme exponentielle
.
Pour écrire $z$, non nul, sous forme exponentielle

Comme pour la forme trigonométrique:
1) Déterminer le module de $z$

Si $z=a+ib$ avec $a$ et $b$ réels:
\[|z|=\sqrt{a^2+b^2}\]

2) Puis un argument de $z$

Si $z=a+ib$ avec $a$ et $b$ réels:
1) On note $\alpha$ un argument de $z$.
2) Puis on utilise les formules:
\[\cos\alpha=\frac a{|z|}\] et \[\sin\alpha=\frac b{|z|}\]
3) On trouve $\alpha$ à l'aide du cercle trigo.

3) Puis remplacer dans la formule $z=re^{i\alpha}$
$r$ par le module de $z$ et $\alpha$ par un argument de $z$.
Si $z=re^{i\alpha}$ alors

Si $z=re^{i\alpha}$ avec r positif et $\alpha$ réel
alors
le module de $z$ vaut $r$ et un argument de $z$ vaut $\alpha$

Si $r$ n'est pas positif, on ne peut pas conclure directement.
Voir les exercices.

\[e^{i(\alpha+\beta)}\]=

\[e^{i(\alpha+\beta)}=e^{i\alpha}e^{i\beta}\]

Même règle que pour les puissances.
$\alpha$ et $\beta$ sont des réels.

\[e^{i(\alpha-\beta)}\]=

\[e^{i(\alpha-\beta)}=\frac{e^{i\alpha}}{e^{i\beta}}\]

Même règle que pour les puissances.
$\alpha$ et $\beta$ sont des réels.

\[\left(e^{i\alpha}\right)^n\]=

\[\left(e^{i\alpha}\right)^n=e^{in\alpha}\]

Même règle que pour les puissances.
$\alpha$ est réel et $n$ est entier.

Cette formule s'appelle la formule de Moivre.

\[\left(e^{i\alpha}\right)^n=e^{in\alpha}\]
écrit sous forme trigonométrique:
\[\left(\cos \alpha+i\sin\alpha\right)^n=\cos(n\alpha)+i\sin(n\alpha)\]

\[\overline{e^{i\alpha}}\]=

\[\overline{e^{i\alpha}}=e^{-i\alpha}\]

$\alpha$ est un nombre réel.

\[e^{i\pi}\]=

\[e^{i\pi}=-1\]

Attention, une exponentielle complexe peut être négative !
Alors qu'une exponentielle réelle est toujours strictement positive.

\[e^{i\frac{\pi}2}\]=

\[e^{i\frac{\pi}2}=i\]

Argument et angle

♦ Cours en vidéo sur l'utilisation des arguments, en particulier en géométrie

Un peu de patience, la vidéo est bientôt prête

\[\arg(z_1z_2)\]=

$\arg(z_1z_2)=\arg(z_1)+\arg(z_2)$ $[2\pi]$

$z_1$ et $z_2$ sont des complexes non nuls

\[\arg(z_1+z_2)\]=

Il n'y a pas de formule pour l'addition.
$\arg(z_1+z_2)$ n'est pas égal à $\arg(z_1)+\arg(z_2)$

\[\arg\left(\frac{z_1}{z_2}\right)\]=

\[\arg\left(\frac{z_1}{z_2}\right)=\arg(z_1)-\arg(z_2)\] $[2\pi]$

$z_1$ et $z_2$ sont des complexes non nuls

\[\arg\left(z^n\right)\]=

\[\arg\left(z^n\right)=n\arg(z)\] $[2\pi]$

$z$ est un complexe non nul
$n$ est un entier.
$\left(\overrightarrow{u};\overrightarrow{\mathrm{AB}}\right)$=

$\left(\overrightarrow{u};\overrightarrow{\mathrm{AB}}\right)=\arg(z_B-z_A)$

A et B sont 2 points distincts
dans un repère orthonormé (O;$\overrightarrow{u}$;$\overrightarrow{v}$).
$z_A$ et $z_B$ sont les affixes respectives de A et B.

\[\left(\overrightarrow{\mathrm{AB}};\overrightarrow{\mathrm{AC}}\right)\]=

\[\left(\overrightarrow{\mathrm{AB}};\overrightarrow{\mathrm{AC}}\right)=\arg\left(\frac{z_C-z_A}{z_B-z_A}\right)\]

A, B et C sont 3 points distincts 2 à 2
dans un repère orthonormé (O;$\overrightarrow{u}$;$\overrightarrow{v}$).
$z_A$, $z_B$, et $z_C$ sont les affixes respectives de A, B et C.

Corrigé en vidéo

Exercices 1:

Lire le module et un argument d'un nombre complexe

- forme trigonométrique - exponentielle

Dans un repère orthonormé direct $\rm \left(O;~\overrightarrow{OD};~\overrightarrow{OE}\right)$, on considère les points A, B, C, D, E, F, G et H.
On note $z_A,~ z_B,~ z_C,~ z_D,~ z_E,~ z_F, ~ z_G,~ z_H$ leurs affixes respectives.

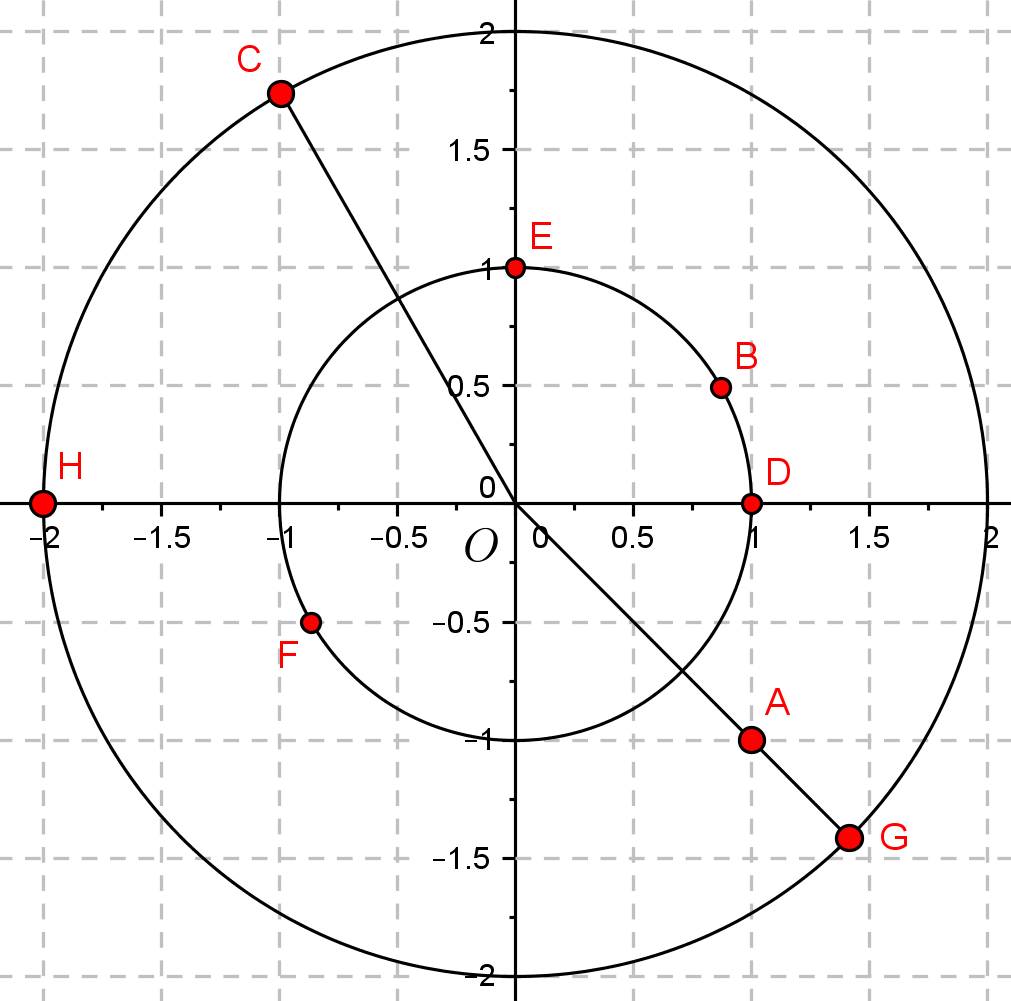
1) Déterminer le module et un argument de $z_A,~ z_B,~ z_C,~ z_D,~ z_E,~ z_F, ~ z_G,~ z_H$.
2) Écrire $z_A,~ z_B,~ z_C,~ z_D,~ z_E,~ z_F, ~ z_G,~ z_H$ sous forme trigonométrique, exponentielle et algébrique.

Corrigé en vidéo

Exercices 2: Déterminer le module et un argument -

forme trigonométrique et exponentielle d'un nombre complexe

1) Déterminer le module et un argument des nombres complexes suivants:

$z_1=3$	$z_2=-4$	$z_3=i$	$z_4=-3i$
$z_5=2+2i$	$z_6=2-2i$	$z_7=-\sqrt 3+3i$

2) Écrire ces nombres complexes sous forme trigonométrique et exponentielle.

Exercices 3:

Propriétés de l'argument d'un nombre complexe

Soit $z$ un nombre complexe non nul.
1) Exprimer $\arg(\overline z)$ en fonction de $\arg(z)$.
2) Exprimer $\arg(-z)$ en fonction de $\arg(z)$.
3) Exprimer $\arg(-\overline z)$ en fonction de $\arg(z)$.

Corrigé en vidéo

Exercices 4: Utiliser les propriétés des arguments d'un nombre complexe

1) Déterminer un argument de $z_1=1+i$ et \[z_2=-3+\sqrt 3i\].
2) En déduire un argument des nombres complexes suivants:

\[z_1\times z_2\]

\[-3-\sqrt 3i\]

\[-\frac12(1+i)\]

\[-1-i\]

\[\frac{(3-\sqrt 3i) ^2}{(1-i)^3}\]

Corrigé en vidéo

Exercices 5: Piège avec les arguments - Ecrire sous forme exponentielle - trigonométrique

Dans chaque cas, donner une forme trigonométrique du nombre complexe $z$:

$z = -2\left( \cos \left(\dfrac{\pi}{12}\right) - i\sin \left(\dfrac{\pi}{12}\right) \right)$
$z = 3\left( \cos \left(\dfrac{\pi}{7}\right) - i\sin \left(\dfrac{\pi}{7}\right) \right)$
$z = 5\left( -\cos \left(\dfrac{\pi}{5}\right) + i\sin \left(\dfrac{\pi}{5}\right) \right)$

Corrigé en vidéo

Exercices 6: Piège avec les arguments - Ecrire sous forme exponentielle - trigonométrique

1) Déterminer le module et un argument des nombres complexes suivants:

\[z_1=2(\cos \frac {\pi} 4+i \sin \frac {\pi} 4)\]	\[z_2=-2(\cos \frac {\pi} 4+i \sin \frac {\pi} 4)\]
\[z_3=2(-\cos \frac {\pi} 4+i \sin \frac {\pi} 4)\]	\[z_4=2(\cos \frac {\pi} 4-i \sin \frac {\pi} 4)\]

2) Écrire ces nombres complexes sous forme exponentielle.

Corrigé en vidéo!

Exercices 7:

Ensemble de points et argument d'un nombre complexe

- lieu de points et argument

Le plan complexe est muni d'un repère orthonormé direct $(O; \overrightarrow{u} ; \overrightarrow{v} )$.
1) Déterminer le lieu des points M d'affixe $z$ tel que \[\arg(z)=\frac \pi 6 ~[2\pi]\].
2) Déterminer le lieu des points M d'affixe $z$ tel que \[\arg(z)=\frac \pi 6 ~[\pi]\].
3) Déterminer le lieu des points M d'affixe $z$ tel que \[\arg(z+i)=-\frac {3\pi} 4 ~[2\pi]\]

Corrigé en vidéo!

Exercices 8: Ecrire un nombre complexe sous forme exponentielle - trigonométrique

Écrire les nombres suivants sous forme exponentielle:

$z_1=2-2i$

\[z_2=-3 \left(\cos \frac \pi 3-i\sin \frac \pi 3\right)\]

\[z_3=\frac 1{-\sqrt 2+i\sqrt 6}\]

Corrigé en vidéo

Exercices 9: Ecrire un nombre complexe sous forme exponentielle - trigonométrique

Écrire les nombres suivants sous forme exponentielle:

\[z_1=-4e^{i\frac \pi 5}\]

\[z_2=\frac{-3(1+i)}{-\sqrt 3+3i}\]

\[z_3=-\sqrt 5 (-2\sqrt 3+6i)^2e^{-i\frac{2\pi} 3}\]

Corrigé en vidéo

Exercices 10:

Equation du second degré à coefficient complexe avec l'exponentielle complexe

Résoudre dans $\mathbb{C}$, l'équation $z^2=-i$.

Corrigé en vidéo Exercices 11:

Problème ouvert - équation du troisième degré et nombre complexe - Racines cubique de l'unité

Résoudre dans $\mathbb{C}$, l'équation $z^3=1$.

Exercices 12: Passer de l'

exponentielle complexe à la forme algébrique

Déterminer la forme algébrique des nombres suivants:

\[z_1=e^{i\pi}\]

\[z_2=e^{i \frac \pi 2}-2e^{i\frac \pi 3}\]

\[z_3=1-e^{-i\frac \pi 2}+3e^{-i\frac \pi 4}\]

\[z_4=\frac {-2e^{i\frac {2\pi}3}}{e^{i\frac \pi 4}}\]

Corrigé en vidéo!

Exercices 13: Nombre complexe et angle - Déterminer un

angle à l'aide des arguments

Le plan complexe est muni d'un repère orthonormé direct $(O; \overrightarrow{u} ; \overrightarrow{v} )$.
On considère les points A et B d'affixes respectives \[z_A=-\sqrt 2-\sqrt 2i\] et \[z_B=\sqrt 3-3i\].
1) Déterminer le module et un argument de $z_A$ et $z_B$.
2) Tracer un repère orthonormé et placer les points A et B à l'aide d'un compas et d'une règle.
3) Déduire de la question 1) une mesure de l'angle ($\overrightarrow {OA}~,~\overrightarrow {OB}$).

Exercices 14: Déterminer l'angle (AB;AC) avec les complexes

Le plan complexe est muni d'un repère orthonormé direct $(O; \overrightarrow{u} ; \overrightarrow{v} )$.
On rappelle que \[\left\{ \begin{array}{l@{~}c@{~}l} \arg\left(\dfrac {z_2}{z_1}\right)=\arg(z_2)-\arg(z_2) \\\\ (\overrightarrow{u};\overrightarrow{AB})=\arg(z_B-z_A) \end{array} \right.\]
A l'aide du rappel, démontrer que \[(\overrightarrow{AB};\overrightarrow{AC})=\arg\left(\frac{z_C-z_A}{z_B-z_A}\right)\].

Corrigé en vidéo

Exercices 15: Lien entre angle et argument - Angle (AB;AC) - Complexe et rectangle

Le plan complexe est muni d'un repère orthonormé direct $(O; \overrightarrow{u} ; \overrightarrow{v} )$. On considère les points A, B, C et D
d'affixes respectives $z_A=-3+i$, $z_B=5-i$, $z_C=6+3i$ et $z_D=-2+5i$.
1) Faire une figure et placer les points A, B, C et D.
2) Quelle conjecture peut-on faire concernant le quadrilatère ABCD.
3) Déterminer l'affixe des vecteurs $\overrightarrow {AB}$ et $\overrightarrow {DC}$. Que peut-on conclure? Justifier.
4) Calculer \[\frac{z_D-z_A}{z_B-z_A}\]. Donner le résultat sous forme algébrique.
5) En déduire une mesure de l'angle ($\overrightarrow {AB},~\overrightarrow {AD}$). Que peut-on en conclure?

Corrigé en vidéo

Exercices 16: cos(pi/12) et sin(pi/12)

Soit \[z_1=1+i\sqrt 3\] et \[z_2=1+i\].
1) Écrire $z_1$ et $z_2$ sous forme trigonométrique et exponentielle.
2) En déduire une forme trigonométrique de $z_1\times z_2$.
3) Déterminer la forme algébrique de $z_1\times z_2$.
4) En déduire la valeur exacte de \[\cos \frac{7\pi}{12}\] et \[\sin \frac{7\pi}{12}\].
5) Que faut-il changer à la méthode précédente pour déduire la valeur exacte de \[\cos \frac{\pi}{12}\] et \[\sin \frac{\pi}{12}\].

Corrigé en vidéo

Exercices 17: Type Bac - Nombre complexe - équation - conjugué - forme exponentielle

On considère l'équation (E): \[z^4=-4\].
1) Montrer que \[z_1=1+i\] est solution de (E).
2) Écrire $z_1$ sous forme exponentielle. Refaire la question 1)
3) Montrer que si $z$ est solution de (E) alors $-z$ et $\overline z$ sont aussi solutions de (E).
4) En déduire trois autres solutions de (E).

Corrigé en vidéo

Exercices 18: Condition pour qu'un nombre complexe soit réel, positif, négatif, imaginaire pur

Soit $n$ un entier naturel.
1) Pour quelles valeurs de $n$, $(1+i)^n$ est-il un réel positif?
2) Pour quelles valeurs de $n$, $(1+i)^n$ est-il un réel?
3) Pour quelles valeurs de $n$, $(1+i)^n$ est-il un imaginaire pur?

Corrigé en vidéo

Exercices 19: Bac Liban 2018 nombre complexe

Pour tout entier naturel $n$, on pose ${\rm S}_n=(1+i)^n+(1-i)^n$.
1) Écrire $1+i$ et $1-i$ sous forme exponentielle.
2) Lætitia affirme que pour tout entier naturel $n$, ${\rm S}_n$ est un nombre réel. A-t-elle raison? Justifier.
3) Existe-il une infinité d'entiers naturels $n$ tels que ${\rm S}_n=0$?

Corrigé en vidéo

Exercices 20: Démontrer un alignement à l'aide des nombres complexes

Le plan complexe est muni d'un repère orthonormé direct $(O; \overrightarrow{u} ; \overrightarrow{v} )$.
À tout point $M$ différent de O, d'affixe $z$, on associe le point $M'$ d'affixe \[z'=-\frac 1{\overline z}\].
Démontrer que $O$, $M$ et $M'$ sont alignés.

Corrigé en vidéo

Exercices 21: Suite de nombres complexes et points alignés

On considère la suite de nombres complexes $(z_n)$ définie pour tout entier naturel $n$ par : $$ \displaystyle z_n=(1-i\sqrt 3)^n$$ Pour tout entier naturel $n$, on note ${\rm M}_n$ le point d'affixe $z_n$.
Pour tout entier naturel $n$, les points ${\rm M}_n,$ ${\rm O}$ et ${\rm M}_{n+3}$ sont-ils alignés?

Exercices 22: Fonction complexe - D'après sujet de Bac

Le plan complexe est muni d'un repère orthonormé direct $(O; \overrightarrow{u} ; \overrightarrow{v} )$.
À tout point $M$ d'affixe $z$, on associe le point $M'$ d'affixe $z'=z^2+4z+3$.
Un point $M$ est dit invariant lorsqu'il est confondu avec le point $M'$ associé.
Démontrer qu'il existe deux points invariants.
Donner l'affixe de chacun de ces points sous forme algébrique, puis sous forme exponentielle.

Exercices 23: Exercice type bac

Le plan complexe est muni d'un repère orthonormé direct $(O; \overrightarrow{u} ; \overrightarrow{v} )$.
A tout point M d'affixe $z$, on associe le point M' d'affixe \[z'=1+z+z^2\].
1) Démontrer que \[e^{i\alpha}+e^{-i\alpha}\] est réel.
2) En déduire que si \[z=e^{i\alpha}\] alors \[\frac{z'}z\] est réel.
3) Que peut-on en déduire concernant les points O, M et M'. Justifier.

Corrigé en vidéo

Exercices 24: Nombre complexe - Type bac - Forme exponentielle - Ensemble de point - Cercle

Le plan complexe est muni d'un repère orthonormé direct $(O; \overrightarrow{u} ; \overrightarrow{v} )$.
A tout point $M$ d'affixe $z$, non nulle, on associe le point $M'$ d'affixe \[z'=\frac 12 (z+\frac 1z)\].
$M'$ est appelé l'image de $M$. $A$ et $B$ sont les points d'affixes respectives -1, 1.
1) Soit le point $C(1;1)$ et $C'$ son image. Déterminer les coordonnées de $C'$.
2) Déterminer les points $M$ tels que $M'=M$.
3) Déterminer les points $M$ qui ont pour image $O$.
4) Démontrer que pour tout réel $\alpha$, \[e^{i\alpha}+e^{-i\alpha}=2\cos \alpha\]
5) En déduire que si $M$ appartient au cercle de centre $O$ et de rayon 1, $M'$ appartient au segment $[AB]$.

Corrigé en vidéo

Exercices 25:

Baccalauréat terminale S métropole septembre 2013

exercice 2

Le plan complexe est muni d'un repère orthonormé direct d'origine O.
On désigne par B et C deux points du plan dont les affixes respectives $b$ et $c$ vérifient l'égalité:
$\displaystyle{ \frac c b=\sqrt 2 e^{i\frac{\pi}{4}} }$
a) Le triangle OBC est-il isocèle en O? Justifier.
b) Les points O,B,C sont-ils alignés? Justifier.
c) Le triangle O,B,C est-il isocèle et rectangle en B? Justifier.

Corrigé en vidéo

Exercices 26:

Bac terminale S Liban 2019

exercice complet révision

Le plan complexe est muni d'un repère orthonormé direct. On appelle $f$ la fonction qui, à tout point $\rm M$, distinct du point O et d'affixe $z$, associe le point $\rm M'$ d'affixe $z'$ tel que $\displaystyle z'=-\frac 1z$.

On considère les points $\rm A$ et $\rm B$ d'affixes respectives $z_{\rm A} = -1+i$ et $\displaystyle z_{\rm B} =\frac 12 e^{i\frac \pi 3}$.
1. Déterminer la forme algébrique de l'affixe du point $\rm A'$ image du point $\rm A$ par la fonction $f$ .
2. Déterminer la forme exponentielle de l'affixe du point $\rm B'$ image du point $\rm B$ par la fonction $f$
3. Placer les points $\rm A$, $\rm B$, $\rm A'$ et $\rm B'$ dans le repère orthonormé direct en laissant les traits de construction apparents.
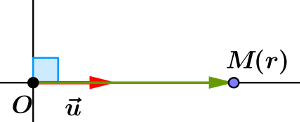
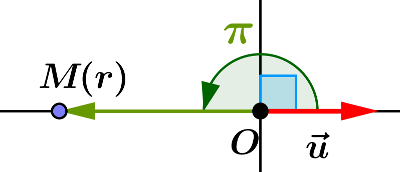
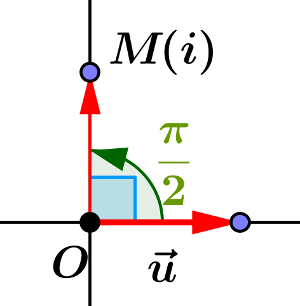
Soit $r$ un réel strictement positif et $\theta$ un réel. On considère le complexe $z$ défini par $z=r e^{i\theta}$.
1. Montrer que $z'=\frac 1r e^{i(\pi-\theta)}$.
2. Est-il vrai que si un point $\rm M$, distinct de 0, appartient au disque de centre 0 et de rayon 1 sans appartenir au cercle de centre 0 et de rayon 1, alors son image $\rm M'$ par la fonction $f$ est à l'extérieur de ce disque ? Justifier.
Soit le cercle $\Gamma$ de centre $\rm K$ d'affixe $z_{\rm K}=-\frac 12$ et de rayon $\frac 12$.
1. Montrer qu'une équation cartésienne du cercle $\Gamma$ est $x^2+x+y^2=0$.
2. Soit $z=x+iy$ avec $x$ et $y$ non tous les deux nuls. Déterminer la forme algébrique de $z'$ en fonction de $x$ et $y$.
3. Soit $\rm M$ un point, distinct de O, du cercle $\Gamma$. Montrer que l'image $\rm M'$ du point $\rm M$ par la fonction $f$ appartient à la droite d'équation $x = 1$.

Corrigé en vidéo

Exercices 27:

Nombre Complexe révision Bac S maths 2019 Pondichéry Centres étrangers Forme exponentielle Géométrie

Le plan est muni d'un repère orthonormé direct $({\rm O};\vec u;\vec v)$. Le but de cet exercice est de déterminer les nombres complexes $z$ non nuls tels que les points $\rm A$, $\rm N$ et $\rm P$ d'affixes respectives $1$, $z^2$ et $\frac 1z$ soient alignés.

Dans cette question, $z=i$. Démontrer que les points $\rm A$, $\rm N$ et $\rm P$ ne sont pas alignés.
Dans cette question, $z=-\frac 12+i\frac{\sqrt 3}2$.
A l'aide de la forme exponentielle de $z$, $z^2$ et $\frac 1z$, démontrer que les points $\rm A$, $\rm N$ et $\rm P$ sont alignés.
Cas général: Soit $z$ un nombre complexe non nul.
1. Établir que, pour tout nombre complexe $z$ différent de $0$, on a $z^2-\frac 1z=(z^2+z+1)\left(1-\frac 1z\right)$.
2. En déduire que, pour $z \ne 0$ , les points $\rm A$, $\rm N$ et $\rm P$ sont alignés si et seulement si $z^2+z+1$ est réel.
3. On pose $z=x+iy$ où $x$ et $y$ sont des réels.
  Déterminer l'ensemble des points $\rm M$ d'affixe $z\ne 0$ tels que les points $\rm A$, $\rm N$ et $\rm P$ soient alignés.
  Tracer cet ensemble.

Exercices 28:

Propriétés du nombres $j$

Le plan complexe est muni d'un repère orthonormé direct $(O; \overrightarrow{u} ; \overrightarrow{v} )$.
Soit le nombre complexe $j=-\frac 12+i\frac{\sqrt 3}2$.
1) Montrer que $j$ est solution de l'équation $z^2+z+1=0$.
2) Écrire $j$ sous forme exponentielle.
3) Démontrer que $j^3=1$ et que $j^2=-1-j$.
4) Soient P, Q et R les points d'affixes respectives 1, $j$ et $j^2$. Quelle est la nature du triangle PQR? Justifier.

Exercices 29:

Problème ouvert - Somme et nombre complexe

Calculer les sommes:
$1+\cos(x)+\cos(2x)+ ... +\cos(nx)$.
$1+\sin(x)+\sin(2x)+ ... +\sin(nx)$.
où $n$ est un entier naturel et $x\in \left]0;\frac{\pi}{2} \right[$.

\(z_1=3\)	\(z_2=-4\)	\(z_3=i\)	\(z_4=-3i\)
\(z_5=2+2i\)	\(z_6=2-2i\)	\(z_7=-\sqrt 3+3i\)