jaicompris.com
Cours et exercices corrigés en vidéo


|
Produit scalaire |

|







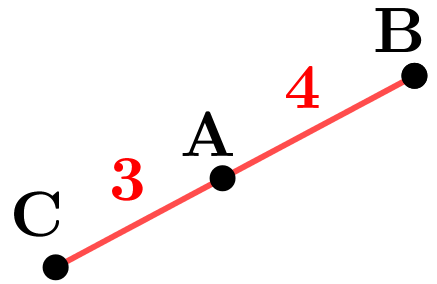 $\color{red}{\textbf{b.
}} $
$\color{red}{\textbf{b.
}} $ 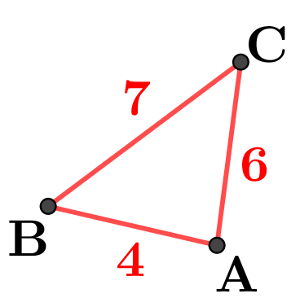 $\color{red}{\textbf{c.
}} $
$\color{red}{\textbf{c.
}} $ 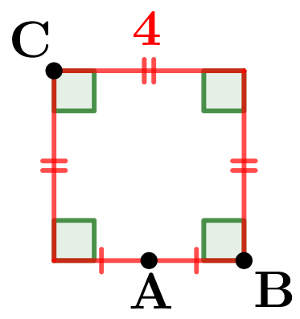 $\color{red}{\textbf{d.
}} $
$\color{red}{\textbf{d.
}} $  $\color{red}{\textbf{e.
}} $
$\color{red}{\textbf{e.
}} $  $\color{red}{\textbf{f.
}} $
$\color{red}{\textbf{f.
}} $