Loi de probabilité continue

Variable aléatoire continue et discrète

♦ Cours en vidéo: comprendre la différence entre discret et continu

L'univers, c'est quoi

Dans une expérience aléatoire, l'univers, c'est l'ensemble de toutes les issues possibles. On le note souvent $\Omega$.

Exemple: On lance 2 dés à 6 faces, numérotées de 1 à 6. Une issue est par exemple (2;5).
Donc $\Omega=\left\{(1;1);(1;2);...;(6;6)\right\}$.
Dans cet exemple, l'univers est composé de 36 issues.
Une variable aléatoire, c'est quoi

Une variable aléatoire est une fonction de l'univers $\Omega$ dans $\mathbb{R}$.

Exemple: On lance 2 dés à 6 faces, numérotées de 1 à 6.
On appelle X la variable aléatoire qui associe à chaque lancer la somme des numéros obtenus.
Donc $\Omega=\left\{(1;1);(1;2);...;(6;6)\right\}$.
X prend donc les valeurs 2, 3,...,12.
Une variable aléatoire discrète, c'est quoi

Lorsque la variable aléatoire ne prend qu'un nombre fini de valeurs,
alors on dit que cette variable aléatoire est discrète.

Exemple: On lance 2 dés à 6 faces, numérotées de 1 à 6.
On appelle X la variable aléatoire qui associe à chaque lancer la somme des numéros obtenus.
Donc $\Omega=\left\{(1;1);(1;2);...;(6;6)\right\}$.
X prend donc les valeurs 2, 3,...,12.
X ne prend que 11 valeurs donc X est discrète.
Une variable aléatoire continue, c'est quoi

Lorsque la variable aléatoire peut prendre toutes les valeurs d'un intervalle,
alors on dit que cette variable aléatoire est continue.

Exemple: On s'interesse à la durée de vie d'un stock de 100 ampoules électriques.
On appelle X la variable aléatoire qui à chaque ampoule associe sa durée de vie.
X peut prendre n'importe quelle valeur de l'intervalle [0;+∞[. Donc X est continue.

♦ Cours en vidéo: comprendre le passage de discret à continu

Densité de probabilité

♦ Cours en vidéo: comprendre la notion de densité

Une densité, c'est quoi

Une densité est une fonction définie sur un intervalle I et qui vérifie 3 conditions:
- Cette fonction doit être continue sur I.
- Cette fonction doit être positive sur I.
- L'aire sous la courbe de cette fonction sur l'intervalle I doit être égale à 1 unité d'aire.
Comment montrer que $f$ est une densité sur [a;b]

1) Vérifier que $f$ est continue sur [a;b].
2) Vérifier que $f$ est positive sur [a;b].

3) Calculer l'aire sous la courbe sur [a;b]

Pour celà,
calculer $\int_{a}^b f(x)~{\rm d}x $
et vérifier que cette intégrale vaut 1.

4) Vérifier que cette aire vaut 1.
Comment montrer que $f$ est une densité sur [a;+∞[

1) Vérifier que $f$ est continue sur [a;+∞[.
2) Vérifier que $f$ est positive sur [a;+∞[.

3) Calculer l'aire sous la courbe sur [a;+∞[

Pour celà,
1) calculer $\int_{a}^t f(x)~{\rm d}x $
2) Calculer $\lim\limits_{t \to +\infty}\int_{a}^t f(x)~{\rm d}x $
3) Vérifier que cette limite vaut 1.
Comment montrer que $f$ est une densité sur $\mathbb{R}$

Une densité sur $\mathbb{R}$ est une fonction qui vérifie 3 conditions:
- Cette fonction doit être continue sur $\mathbb{R}$.
- Cette fonction doit être positive sur $\mathbb{R}$.
- L'aire sous la courbe de cette fonction sur l'intervalle $\mathbb{R}$ doit être égale à 1 unité d'aire.

Autrement dit, si cette fonction s'appelle $f$:
$\lim\limits_{t \to +\infty}\int_{0}^t f(x)~{\rm d}x+\lim\limits_{t \to -\infty}\int_{t}^0 f(x)~{\rm d}x =1$

Loi de probabilité à densité

♦ Cours en vidéo: Comprendre et savoir calculer des probabilités avec une loi continue

Dire que X suit une loi de densité $f$ sur I signifie

La probabilité $\rm P(X\in J)$ est égale à l'aire sous la courbe de $f$ sur l'intervalle J
X suit une loi de densité $f$ sur I alors:
${\rm P}(a\le {\rm X}\le b)=$

${\rm P}(a\le {\rm X}\le b)=\int_{a}^b f(x)~{\rm d}x$

${\rm P}({\rm X}=k)=$

${\rm P}({\rm X}=k)=0$

${\rm P}({\rm X}=k)=\int_k^k f(x)~{\rm d}x=0$

${\rm P}(a\le {\rm X}\le b)$ se note aussi

${\rm P(X\in }[a;b])$

${\rm P}(a\lt {\rm X}\le b)$=

${\rm P}(a\lt {\rm X}\le b)={\rm P}(a\le {\rm X}\lt b)={\rm P}(a\lt {\rm X}\lt b)={\rm P}(a\le {\rm X}\le b)=\int_{a}^b f(x)~{\rm d}x$

Cela vient du fait que dans le cas continu, comme $P(X=k)=0$,
enlever un seul nombre de l'intervalle, ne change pas la probabilité.
Attention, c'est faux dans le cas discret.

Si I=[-2;+∞[ alors $\rm P(X\ge 3)$=

${\rm P(X\ge 3)=1-P(X\lt 3)=1-P(X\le 3)}=1-\int_{-2}^{3} f(t)~{\rm d}t$

Espérance d'une variable aléatoire continue

♦ Cours en vidéo: comprendre et savoir déterminer l'espérance d'une variable aléatoire continue

X de densité $f$ sur [a;b] alors l'espérance de X

notée E(X)=$\int_a^b xf(x)~{\rm d}x$

Dans le cas discret:	${\rm E(X)}=\sum_{i=1}^n x_i p({\rm X}=x_i)$
Dans le cas continu:	${\rm E(X)}=\int_a^b xf(x)~{\rm d}x$

Pour passer du cas discret au continu:
- remplacer le symbole somme $\sum$ par intégral $\int$.
- remplacer la probabilité $P({\rm X}=x_i)$ par la densité $f$.

X de densité $f$ sur [a;+∞[ alors l'espérance de X

notée E(X)=$\lim\limits_{t \to +\infty}\int_a^t xf(x)~{\rm d}x$

Sous réserve que cette limite existe!
X de densité $f$ sur $\mathbb{R}$ alors l'espérance de X

notée E(X)=$\lim\limits_{t \to +\infty}\int_0^t xf(x)~{\rm d}x+\lim\limits_{t \to -\infty}\int_t^0 xf(x)~{\rm d}x$

Sous réserve que ces 2 limites existent!

Corrigé en vidéo

Exercices 1:

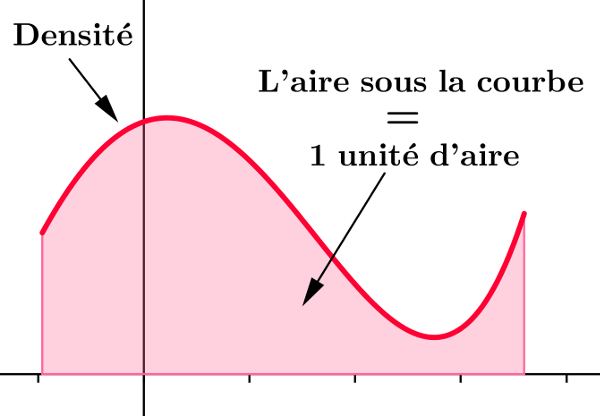
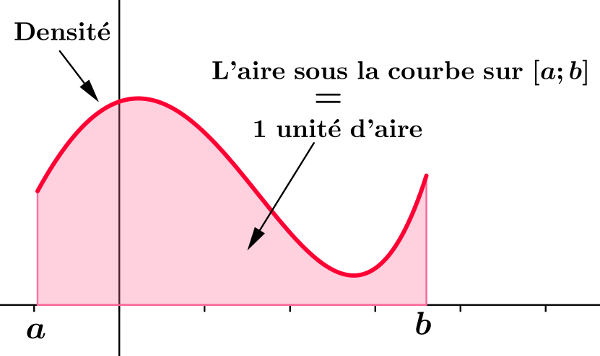
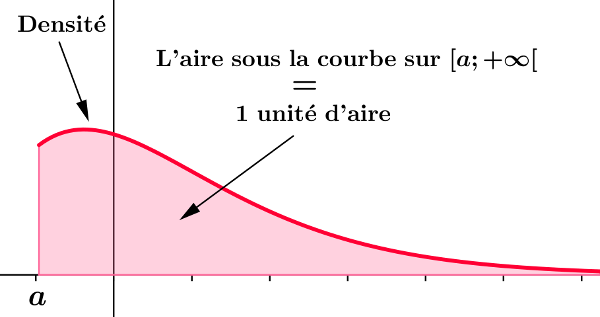
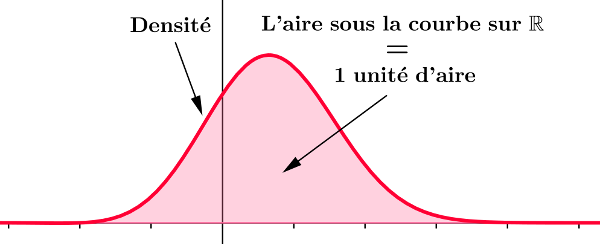
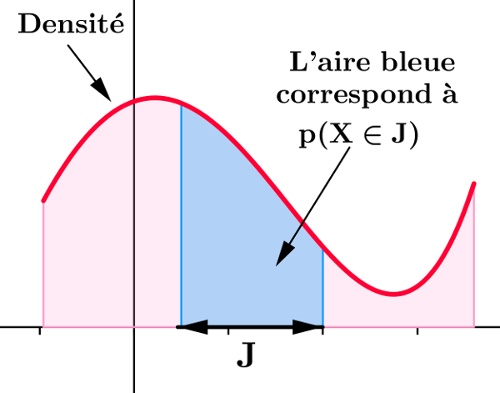
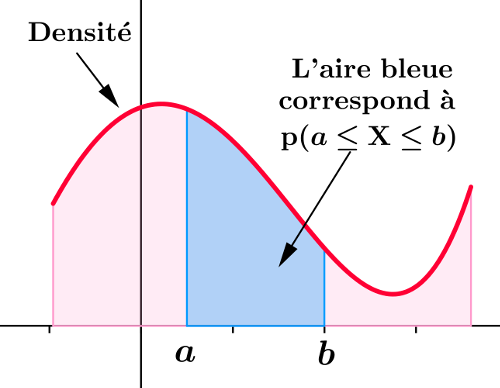
Densité de probabilité

Dans chaque cas, justifier que la fonction $f$ est une densité de probabilité sur l'intervalle I indiqué:
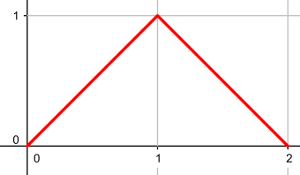
1) $f$ est définie sur I=[0;2] par sa courbe ci-contre:
2) $f$ est définie sur I=[-1;1] par $f(x)=\frac{3}{4}-\frac{3}{4}x^2$.
3) $f$ est définie sur I=[0;+$\infty$[ par $f(x)=e^{-x}$.

Corrigé en vidéo

Exercices 2: Calculer des probabilités avec une variable aléatoire continue

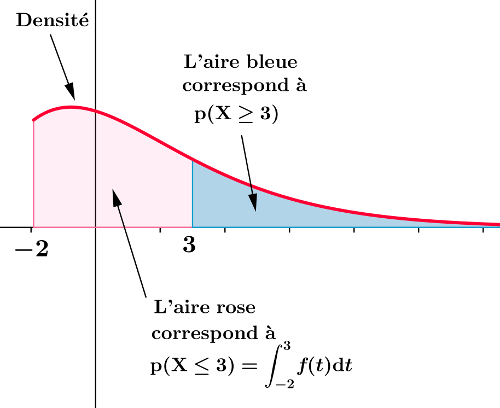
On considère la fonction $f$ définie sur $[0;+\infty[$ par $f(x)=e^{-x}$. X est une variable aléatoire de densité $f$.
Calculer les probabilités suivantes: a) $\rm P(1\le X\le 2)$ b) $\rm P(X\ge 3)$.

Corrigé en vidéo

Exercices 3:

Probabilité conditionnelle et

densité de probabilité

On considère la fonction $f$ définie sur $[0;4]$ par $f(x)=\frac{1}{8}x$.
1) Vérifier que $f$ est bien une densité de probabilité sur [0;4].
2) Soit X est une variable aléatoire de densité $f$. Déterminer la probabilité: $\rm P_{X\ge 2}(1\le X\le 3)$.
3) Les évènements $\rm(X\ge 2)$ et $\rm (1\le X\le 3)$ sont-ils indépendants?

Corrigé en vidéo

Exercices 4:

Densité de probabilité

et fonction trigonométrique

On considère la fonction $f$ définie sur $\left[-\frac{\pi}{2};\frac{\pi}{2}\right]$ par $f(x)=k\cos x$ où $k\in \mathbb{R}$.
1) Déterminer le réel $k$ tel que $f$ soit une densité de probabilité sur $\left[-\frac{\pi}{2};\frac{\pi}{2}\right]$.
2) Déterminer le réel $a\in \left[-\frac{\pi}{2};\frac{\pi}{2}\right]$ tel que ${\rm P(}-a\le {\rm X}\le a)=\frac{1}{2}$.

Exercices 5:

On considère la fonction $f$ définie sur $\left[1;5\right]$ par $f(x)=\frac{k}{t^2}$ où $k\in \mathbb{R}$.
1) Déterminer le réel $k$ tel que $f$ soit une densité de probabilité sur $\left[1;5\right]$.
2) Déterminer le réel $a$ tel que ${\rm P(X}\le a)={\rm P(X}\ge a)$.

Corrigé en vidéo

Exercices 6:

Espérance d'une variable aléatoire continue

Soit X une variable aléatoire de densité $f$ définie sur [0;3] par $f(x)=\frac{1}{9}x^2$.
Déterminer E(X).

Corrigé en vidéo

Exercice 7: Espérance sur un intervalle non borné

On considère la fonction $f$ définie sur $[1;+\infty[$ par $f(x)=\frac{2}{x^3}$.
1) Vérifier que $f$ est bien une densité de probabilité sur $[1;+\infty[$.
2) Soit X une variable aléatoire de densité $f$. Déterminer l'espérance de X, notée E(X).

Exercice 8:

On considère la fonction $f$ définie sur $[1;2]$ par $f(x)=\frac{2}{x^2}$.
1) Vérifier que $f$ est bien une densité de probabilité sur $[1;2]$.
2) Soit X une variable aléatoire de densité $f$. Déterminer l'espérance de X, notée E(X).

Corrigé en vidéo

Exercice 9:

On considère la fonction $f$ définie sur $\left[0;\frac{\pi}{2}\right]$ par $f(x)=\cos x$.
1) Vérifier que $f$ est bien une densité sur $\left[0;\frac{\pi}{2}\right]$.
2) Soient les fonctions $g$ et $G$ définies sur $\left[0;\frac{\pi}{2}\right]$ respectivement par
$g(x)=x\cos x$ et $G(x)=ax\sin x+b\cos x$, où $a$ et $b$ sont des réels.
Déterminer $a$ et $b$ tels que la fonction $G$ soit une primitive de $g$.
3) Soit X une variable aléatoire de densité $f$. Déterminer l'espérance de X, notée E(X).

Lois de probabilité continues - Densité

Variable aléatoire continue et discrète

Densité de probabilité

Loi de probabilité à densité

Espérance d'une variable aléatoire continue

Densité de probabilité

densité de probabilité

Densité de probabilité

Espérance d'une variable aléatoire continue