Corrigé en vidéo
Exercices 1:
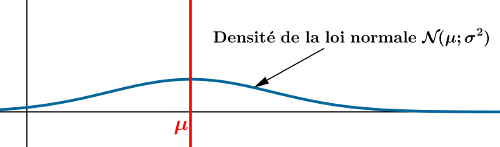
Loi normale et symétrie
Une variable aléatoire X suit une loi normale d'espérance 45. On sait que $\rm P(X>30)=0,7$.
Déterminer, sans calculatrice, les probabilités suivantes: $\rm P(X\geqslant 60)$ $\rm P(30 \leqslant X\leqslant 60)$



Exercices 2:
Loi normale et calculatrice
Une variable aléatoire X suit la loi normale $\mathcal{N}(80;49)$. Déterminer les probabilités suivantes à $10^{-2}$ près:
$\rm P(X<80)$ $ \rm P(X\geqslant 85)$
$ \rm P(80\leqslant X\leqslant 85)$ $ \rm P(X< 80\cup X> 85)$$\rm P_{X\leqslant 85}(X\geqslant 80)$



Corrigé en vidéo
Exercices 3:
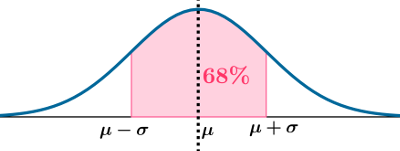
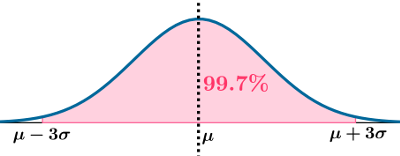
Cours : 1, 2, 3 sigmas
Une variable aléatoire X suit la loi normale $\mathcal{N}(\mu;\sigma^2)$. Déterminer les probabilités suivantes à $10^{-3}$ près:
${\rm P}(\mu-\sigma\leqslant {\rm X}\leqslant\mu+\sigma)$
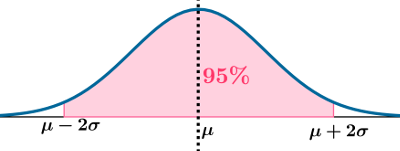
${\rm P}(\mu-2\sigma\leqslant {\rm X}\leqslant\mu+2\sigma)$
${\rm P}(\mu-3\sigma\leqslant {\rm X}\leqslant\mu+3\sigma)$



Corrigé en vidéo
Exercices 4:
Loi normale: déterminer l'espérance $\mu$
Une étude a permis de révéler que le score d'un candidat lors d'un test, peut être modélisé par une variable aléatoire $\rm X$ qui suit une loi normale d'écart-type 20.
Dans chaque cas, Déterminer l'espérance $\mu$ à $10^{-2}$ près.
a) 80 % des candidats ont un score inférieur à 60 points.
b) 30 % des candidats ont un score supérieur à 70 points.



Corrigé en vidéo
Exercices 5:
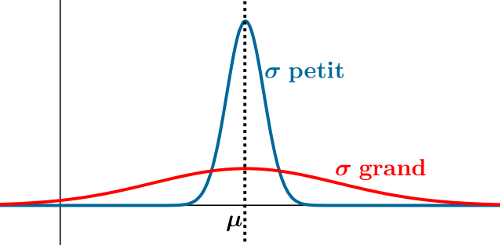
Loi normale: déterminer l'écart-type $\sigma$
Une étude a permis de révéler que le retard d'un train, en minute, peut être modélisé par une variable aléatoire $\rm X$ qui suit une loi normale d'espérance 5.
10% des trains ont plus de 15 minutes de retard. Déterminer l'écart-type $\sigma$ à $10^{-2}$ près.



Corrigé en vidéo
Exercices 6:
Loi normale et probabilité conditionnelle
Une étude a permis de révéler que le retard d'un train, en minute, peut être modélisé par une variable aléatoire $\rm X$
qui suit une loi normale d'espérance 5.
On a observé que 80% des trains ont moins de 7 minutes de retard.
Un train a déjà 3 minutes de retard.
Déterminer, sans calculatrice, la probabilité que ce train ait moins de 7 minutes de retard.



Corrigé en vidéo
Exercices 7:
Loi normale: déterminer l'espérance $\mu$ et l'écart-type $\sigma$
La durée de vie d'une ampoule, en heure, suit une loi normale $\mathcal{N}(\mu;\sigma ^2)$.
On a observé que 80% des ampoules ont une durée de vie supérieure à 3000h
et 10% ont une durée de vie inférieure à 1000h.
Déterminer l'espérance $\mu$ et l'écart-type $\sigma$.
On arrondira les résultats obtenus à la calculatrice au centième.



Corrigé en vidéo
Exercices 8:
Loi normale et QI
Les tests de QI sont conçus de façon à ce que la répartition des QI suive la loi normale $\mathcal{N}(100;225)$.
On considère qu'un individu est surdoué s'il fait partie des 5% de la population ayant le QI le plus élevé.
A partir de quel QI est-on considéré comme surdoué?



Corrigé en vidéo
Exercices 9:
Loi normale et intervalle
On a observé que la taille des basketteurs T, en cm, suit la loi normale $\mathcal{N}(190;36)$.
1) Déterminer sans calcul, un intervalle dans lequel la taille d'un basketteur pris au hasard
a environ 68% de chances de se trouver.
2) Un sélectionneur décide de choisir des basketteurs. Pour cela, il cherche un intervalle centré en 190,
dans lequel la taille d'un basketteur a 90% de chances de se retrouver. Déterminer cet intervalle.



Corrigé en vidéo
Exercices 10:
Loi normale et taille
Un boulanger fabrique des baquettes dont la taille T, en gramme, suit une loi normale d'espérance 200.
Il affirme que 95% de ses baguettes font entre 190 et 210 grammes.
1) Déterminer, sans calculatrice, une valeur approchée de l'écart-type $\sigma$.
2) Déterminer, sans calculatrice, la probabilité d'avoir une baguette qui pèse moins de 190 g.
3) Quelle est la probabilité d'avoir deux jours d'affilée une baguette qui pèse moins de 190 g?



Exercices 11:
Loi normale et réglage d'une machine
Une machine fabrique des tubes métalliques cylindriques.
Les diamètres, en millimètre, des tubes sont distribués suivant une loi normale $\mathcal{N}(15;9)$.
Pour être utilisables, les tubes doivent avoir un diamètre compris entre 14 et 16 millimètres.
1) Quelle est la probabilité qu'un tube ne soit pas utilisable.
2) Un ingénieur affirme qu'en modifiant la machine, il peut réduire l'écart-type.
Quel devrait-être cet écart-type pour que 95% des tubes soient utilisables?



Corrigé en vidéo
Exercices 12:
Loi normale et réglage d'une machine
Des sachets sont remplis de poudre par une machine.
On pose une étiquette sur chaque sachet, indiquant qu'il contient 100 grammes de poudre. On observe que la masse M d'un sachet suit une loi normale
d'écart-type $\sigma=2$. La valeur de l'espérance $\mu$, dépend du réglage de la machine.
Sur quelle valeur de $\mu$ faut-il régler la machine pour que 99% des sachets aient une masse supérieure
à 100 g?



Corrigé en vidéo
Exercices 13:
loi normale - savoir trouver les paramètres μ et σ - Bac S Liban 2017 Exercice 2 Partie A
La durée de stationnement d’une voiture dans un parking de centre-ville est modélisée par une variable
aléatoire $\rm T$ qui suit une loi normale d’espérance $\mu$ et d’écart-type $\sigma$.
On sait que la moyenne du temps de stationnement dans ce parking est égale à 30 minutes et que
75% des voitures ont un temps de stationnement inférieur à 37 minutes.
Le gestionnaire du parking vise l’objectif que 95% des voitures aient un temps de stationnement
entre 10 et 50 minutes. Cet objectif est-il atteint ?
Dans tout l’exercice, les probabilités seront données avec une précision de $10^{-4}$



Corrigé en vidéo
Exercices 14:
loi normale - espérance - Loi de probabilité - Bac S Liban 2017 Exercice 2 partie B
Dans un parking, la durée de stationnement d’une voiture est modélisée par une variable aléatoire $\rm D$ qui suit la loi normale d’espérance $\mu = 70$ min et d’écart-type $\sigma = 30$ min. La durée de stationnement est limitée à trois heures. Les tarifs sont indiqués dans le tableau ci-dessous. Toute heure commencée est due intégralement.
| Durée de stationnement |
Inférieure à 15 min | Entre 15 min et 1h |
Heure supplémentaire |
| Tarif en euros |
Gratuit |
3,5 |
$t$ |
Déterminer le tarif $t$ de l’heure supplémentaire que doit fixer le gestionnaire du parking pour que le prix moyen de stationnement d’une voiture soit de $5$ euros.
Dans tout l’exercice, les probabilités seront données avec une précision de $10^{-4}$.



Corrigé en vidéo
Exercices 15:
loi normale - Trouver l'écart connaissant l'espérance - Inverse normale
Le diamètre d’une bille prélevée au hasard dans la production d'une machine est modélisé à l’aide d’une variable aléatoire Y qui suit une loi normale d’espérance $\mu=1$ et d’écart-type $\sigma$.
Sachant que $\rm P(0,9 \le Y\le 1,1)=0,98$, déterminer une valeur approchée au millième de $\sigma$.