Corrigé en vidéo!
Exercices
1:
Étude complète d'une fonction logarithme
On considère la fonction $f$ définie sur $\mathbb{R}$ par $f(x)=\ln(x^2+1)-x$.
-
Déterminer la fonction dérivée de $f$.
-
Étudier les variations de la fonction $f$.
-
Étudier la limite de $f$ en $-\infty$.
-
Montrer que pour tout $x\gt 0$, $f(x)=2\ln x+\ln\left(1+\dfrac 1{x^2}\right)-x$.
En déduire la limite de $f$ en $+\infty$.
-
Dresser le tableau de variations de $f$
-
En déduire le signe de $f(x)$ en fonction de $x$.


Corrigé en vidéo!
Exercices
2:
Étude complète d'une fonction logarithme
On considère la fonction $f$ définie sur $]0;+\infty[$ par $f(x)=\dfrac{x-1}{x} \ln(x)$.
On note $\mathscr{C}$ la courbe représentative de $f$ dans un repère orthonormé.
-
-
Étudier le sens de variation de la fonction $g$ définie sur $]0;+\infty[$ par
$g(x)=x-1+\ln x$.
-
Vérifier que $g(1)=0$. En déduire selon les valeurs de $x$, le signe de $g(x)$.
-
-
Montrer que pour $x\gt 0$, $f'(x)=\dfrac {g(x)}{x^2}$.
-
En déduire les variations de $f$.
-
Étudier la limite de $f$ en $0$ puis en $+\infty$.


Exercices
3:
Déterminer a, b connaissant la courbe de f - (ax+b) ln x
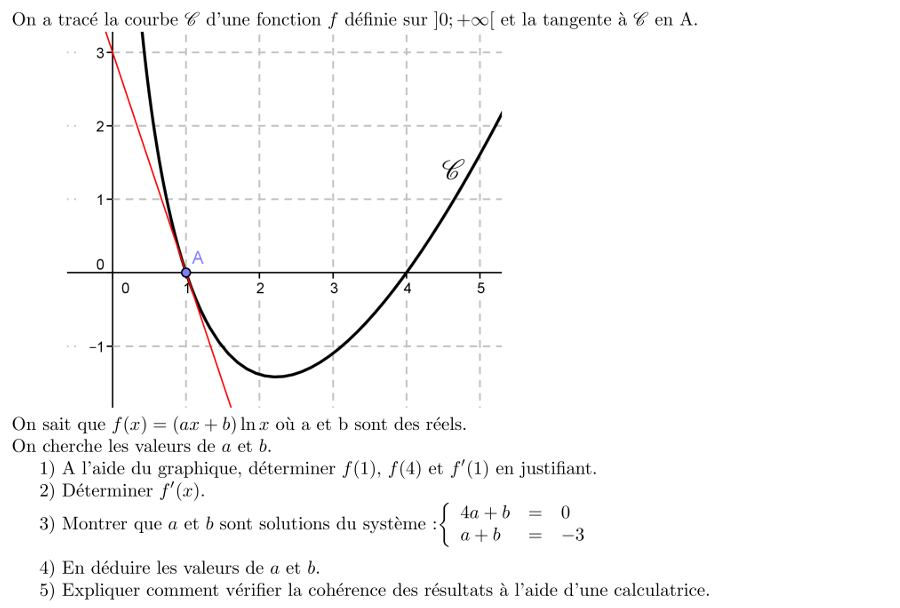


Corrigé en vidéo!
Exercices
4:
Position relative de 2 courbes - logarithme - D'après sujet de Bac
On considère les fonctions $f$ et $g$ définies sur $]0;+\infty[$ par $f(x)=\ln x$ et $g(x)=(\ln x)^2$.
On note $\mathscr{C}_f$ et $\mathscr{C}_g$ les courbes représentatives de $f$ et $g$.
1) Étudier les positions relatives de $\mathscr{C}_f$ et $\mathscr{C}_g$.
2) Soit M et N les points de $\mathscr{C}_f$ et $\mathscr{C}_g$ d'abscisse $x$. Sur
l'intervalle $[1;e]$, pour quelle valeur de $x$,
la distance MN est-elle maximale? Quelle est la valeur de
cette distance maximale?


Corrigé en vidéo!
Exercices
5:
Aire maximale d'un rectangle - Fonction logarithme - D'après sujet
de Bac - Problème ouvert
Soit $f$ la fonction définie sur ]0 ; 14] par $f (x) = 2-\ln\left(\frac x2 \right)$ dont la courbe
$\mathscr{C}_f$ est donnée dans le repère orthogonal d’origine O ci-dessous :

À tout point M appartenant à $\mathscr{C}_f$, on
associe le point P projeté orthogonal de M sur l’axe des abscisses, et le point Q projeté orthogonal de M
sur l’axe des ordonnées.
• $f$ est-elle positive sur $]0;14]$?
• L'aire du rectangle OPMQ est-elle constante, quelle que soit la position du
point M sur $\mathscr{C}_f$ ?
• L’aire du rectangle OPMQ peut-elle être maximale ? Si oui, préciser les
coordonnées
du point M correspondant. Justifier les réponses.


Corrigé en vidéo!
Exercices
6:
Suite et logarithme
- u
n+1=f(u
n) -
u
n+1=√u
n - Exercice type Bac



Corrigé en vidéo!
Exercices
7:
Fonction logarithme népérien
-
Fonction auxiliaire
-
théorème des valeurs intermédiaires

Indication:
Calculer u(α) de 2 façons
En déduire que α+2 = ....
Puis calculer f(α) et conclure



Exercices
8: Position relative de 2 courbes - logarithme



Exercices
9: Suite et logarithme - un+1=f(un)



Exercices
10: Logarithme et équation - ln x=-x - théorème des valeurs
intermédiaires
On a tracé la courbe de la fonction logarithme népérien.
1. Résoudre graphiquement l'équation $\ln x=-x$.
2. Montrer que l'équation $\ln x=-x$ admet une seule solution $\alpha$ sur $]0;+\infty[$.
3. Déterminer un encadrement de $\alpha$ d'amplitude $10^{-2}$.



Corrigé en vidéo
Exercices
11:
Equation avec paramètre - nombre de solution
On considère l'équation $\rm (E_1)$ : $\displaystyle e^x-x^n=0$.
où $x$ est un réel strictement positif et $n$ un entier naturel non nul.
1. Montrer que l'équation $\rm (E_1)$ est équivalente à l'équation $\rm (E_2)$ : $\displaystyle {\ln
(x)-\frac xn=0}$.
2. Pour quelles valeurs de $n$ l'équation $\rm (E_1)$ admet-elle deux solutions ?



Corrigé en vidéo!
Exercices
12:
Problème ouvert - Sujet de Bac Liban 2015 exercice 3
On considère la courbe $\mathscr{C}$ d'équation $y=e^x$, tracée ci-contre:
Pour tout réel $m$ strictement positif, on note $\mathscr{D}_m$ la droite d'équation $y = mx$.
1. Dans cette question, on choisit $m = e$.
Démontrer que la droite $\mathscr{D}_e$ d'équation $y = ex$,
est tangente à la courbe $\mathscr{C}$ en son point d'abscisse 1.
2. Conjecturer, selon les valeurs prises par le réel strictement positif $m$,
le nombre de points d'intersection de la courbe $\mathscr{C}$ et de la droite
$\mathscr{D}_m$.
3. Démontrer cette conjecture.



Corrigé en vidéo!
Exercices
13:
QCM révision logarithme népérien - type bac
Dire si les affirmations sont vraies ou fausses. Justifier.
1. L'équation $\ln x=-1$ n'a pas de solution.
2. Si $u>0$ alors $\ln u>0$.
3. $\ln (x^2)$ peut être négatif.
4. Pour tout $x>0$, $\ln(2x)>\ln x$
5. L'expression $\ln (-x)$ n'a pas de sens.
6. Pour tous réels $x$ et $y$ strictement positifs, $\ln x \times \ln y=\ln(x+y)$.
7. Si $f(x)=(\ln x)^2$ alors $f'(x)=\frac{2\ln x}x$.
8. ($u_n$) est une suite géométrique avec $u_0>0$ et la raison $q>0$ alors $\left(\ln(u_n)\right)$ est
arithmétique.


Exercices
14:
Question ouverte - Comparaison de exponentielle et logarithme
Démontrer que pour tout réel $x>0$, $e^x>\ln x$.


Corrigé en vidéo!
Exercices
15:
fonction exponentielle avec paramètre - Bac S Amérique du nord
2017 exercice 2
Soit $f$ définie sur $[-2;2]$ par $f (x)=-\frac b8\left(e^{^{\textstyle{\frac
xb}}}+e^{^{\textstyle{-\frac xb}}}\right)+ \frac 94$ où $b > 0$.
-
Montrer que, pour tout réel $x$ appartenant à l’intervalle [-2 ; 2], $f (-x) = f (x)$.
Que peut-on en déduire pour la courbe de $f$ ?
-
Montrer que pour tout $x$ de l'intervalle $[-2;2]$, $f'(x)=-\frac 18\left(e^{^{\textstyle{\frac
xb}}}-e^{^{\textstyle{-\frac xb}}}\right)$.
-
Dresser le tableau de variations de $f$ sur l’intervalle [-2 ; 2]


Corrigé en vidéo!
Exercices
16:
fonction exponentielle, minimum et points alignés - Bac S Liban
2017 exercice 3
Soit $k$ un réel strictement positif. On considère les fonctions $f_k$ définies sur $\mathbb{R}$ par
$f_k(x)=x+ke^{-x}$.
On note $\mathscr{C}_k$ la courbe représentative de la fonction $f_k$ dans un plan muni d’un repère
orthonormé.
On a représenté ci-dessous quelques courbes $\mathscr{C}_k$ pour différentes valeurs de $k$.

Il semblerait que chaque fonction $f_k$ admette un minimum sur $\mathbb{R}$. Si l'on appelle $A_k$ le
point de $\mathscr{C}_k$ correspondant à ce minimum, il semblerait que ces points $A_k$ soient alignés.
Est-ce le cas ?


Corrigé en vidéo!
Exercices
17:
Logarithme - hauteur maximum et angle de tir - Amérique du Nord
Bac 2018

On lance un projectile dans un milieu fluide. On modélise le projectile par
un point qui se déplace sur la courbe représentative de la fonction $f$
définie sur l'intervalle
$[0; 1[$ par :
$f(x)=bx+2\ln (1-x)$
où $b$ est un paramètre réel supérieur ou égal à 2, $x$ est l'abscisse du
projectile, $f (x)$ son ordonnée, toutes les deux exprimées en mètres.
$f$ est dérivable sur
[0;1[.
- Montrer que pour tout $x\in [0;1[$, $\displaystyle f'(x)=\frac{-bx+b-2}{1-x}$.
- En déduire le tableau de variations de $f$ sur $[0;1[$.
- Déterminer pour quelles valeurs du paramètre $b$ la hauteur maximale
du projectile ne
dépasse pas $1,6$ mètre.
- Dans cette question, on choisit $b = 5,69$.
L'angle de tir $\theta$ correspond à l'angle entre l'axe des abscisses et
la tangente à la courbe de la
fonction $f$ au point d'abscisse 0 comme indiqué sur le schéma donné ci-contre.
Déterminer une valeur approchée au dixième de degré près de l'angle $\theta$



Corrigé en vidéo!
Exercices
18:
Fonction Logarithme népérien - aire maximale d'un triangle Bac
Liban 2019

Le plan est muni d'un repère orthogonal (O,I,J). On note $\Gamma$ la courbe représentative de la
fonction $g$ définie sur $]0; 1]$ par $g(x)=\ln x$.
Soit $a\in ]0; 1]$. On note ${\rm M}_a$ le point de la courbe $\Gamma$ d'abscisse $a$ et $d_a$ la
tangente à
la courbe $\Gamma$ au point ${\rm M}_a$. Cette droite $d_a$ coupe l'axe des abscisses au point ${\rm
N}_a$ et l'axe des ordonnées
au point ${\rm P}_a$.
On s'intéresse à l'aire du triangle ${\rm ON}_a{\rm P}_a$ quand $a$ varie dans $]0;1]$
- Dans cette question, on étudie le cas particulier où $a = 0,2$ et
on donne la figure
ci-contre:
- Déterminer graphiquement une estimation de l'aire
du triangle ${\rm ON}_{0,2}{\rm P}_{0,2}$ en unités d'aire.
- Déterminer une équation de la tangente $d_{0,2}$.
- Calculer la valeur exacte de l'aire du triangle $\rm ON_{0,2}P_{0,2}$ .
- On admet que, pour tout réel a de $]0;1]$, l'aire en unité d'aire
du triangle ${\rm
ON}_a{\rm P}_a$ est donnée par $\mathscr{A}(a)=\frac 12 a(1-\ln a)^2$.
Déterminer l'aire maximale du triangle ${\rm ON}_a{\rm P}_a$.



Corrigé en vidéo!
Exercices
19:
logarithme suite Révision Dérivation Récurrence limite
algorithme Bac S maths Amérique du Nord 2019

Sur l'intervalle $[0;+\infty [$, on définit la fonction $f$ par $f(x)=x-\ln (x +1)$.
-
- Étudier le sens de variation de la fonction $f$.
- En déduire que pour tout $x\in [0 ; +\infty[$, $\ln(x +1) \leqslant x$.
- On pose $u_0 = 1$ et pour tout entier naturel $n$, $u_{n+1} = u_n -\ln(1+ u_n )$.
On admet que la suite $(u_n)$ est bien définie.
- Calculer une valeur approchée à $10^{-3}$ près de $u_2$.
- Démontrer par récurrence que pour tout entier naturel $n$, $u_n \geqslant 0$.
- Démontrer que la suite $(u_n)$ est décroissante, et en déduire que pour tout entier
naturel $n$, $u_n\leqslant 1$.
- Montrer que la suite $(u_n)$ est convergente.
- On note $\ell$ la limite de la suite $(u_n)$ et on admet que $\ell = f(\ell)$. En
déduire la valeur de $\ell$.
- Écrire un algorithme qui, pour un entier naturel $p$ donné, permet de déterminer le plus
petit rang $\rm N$ à partir
duquel tous les termes de la suite $(u_n)$ sont inférieurs à $10^{-p}$.






 pour avoir une vision d'ensemble
pour avoir une vision d'ensemble
 pour avoir une approche rigoureurse
pour avoir une approche rigoureurse






















































