Dérivation - compléments

Dans chaque cas, calculer la dérivée de la fonction sur l'intervalle I indiqué:
    a) \[f(x)=\frac{5x^4}2-\frac 3{4x^2}-\frac23\] et I=$]-\infty;0[$.
    b) \[f(t)=\frac 5{(t^2+1)^3}\] et I=$\mathbb{R}$.

Calculer la dérivée de la fonction $f$ définie sur $]0;+\infty[$ par \[f(x)=\left(3+\frac 2x-\frac1{x^2}\right)^2\].

Calculer la dérivée de la fonction $f$ définie sur $]-\infty;1[$ par \[f(t)=\left(\frac {t+2}{t-1}\right)^2\].

Calculer la dérivée de la fonction $f$ définie sur $\mathbb{R}$ par \[f(x)=(2x-3)^4\left(1-x^2\right)^7\].

On considère la fonction $f$ définie sur $[-1;2]$ par \[f(x)=\sqrt{-x^2+x+2}\].
1) Justifier que $f$ est dérivable sur $]-1;2[$.
2) Pour tout $x$ de $]-1;2[$, calculer $f'(x)$.

On rappelle que :
        Si $u$ et $v$ sont deux fonctions dérivables sur un intervalle I
        alors $\left\{\begin{array}{l} \text{la fonction } u\times v \text{ est dérivable sur I}\\ (u\times v)'=u'v+uv' \end{array}\right.$

Soit $u$ une fonction dérivable sur I.
    1) Démontrer que $u^2$ est dérivable sur I et déterminer $\left(u^2\right)'$.
    2) Démontrer que $u^3$ est dérivable sur I et déterminer $\left(u^3\right)'$.
    3) Quelles conjectures peut-on faire?
    4) Démontrer ces conjectures.

1) Soit $f$ la fonction définie sur $[0;+\infty[$ par $f(x)=\sqrt x$. Justifier que $f$ n'est pas dérivable en 0.
2) Soit $g$ la fonction définie sur $[0;+\infty[$ par $f(x)=x\sqrt x$. Justifier que $g$ est dérivable en 0.

Pour tout entier $n\ge 1$, on note la fonction $f_n$ définie sur $\mathbb{R}$ par $f(x)=(x^2-2x)^n$.
Déterminer les variations des fonctions $f_n$ selon les valeurs de $n$.

Pour tout entier $n\ge 1$, on note la fonction $f_n$ définie sur $\mathbb{R}$ par $f(x)=(x^2-2x)^n$.
Démontrer que toutes les courbes représentatives des fonctions $f_n$ passent par 4 points fixes,
c'est à dire dont les coordonnées ne dépendent pas de $n$. Donner les coordonnées de ces 4 points fixes.

On considère la fonction $f$ définie $\mathbb{R}$ par $f(x)=\sqrt{x^2+3}$ et on note $\mathscr{C}$ sa courbe représentative.
1) Justifier que $f$ est dérivable sur $\mathbb{R}$ et calculer sa dérivée.
2) Existe-t-il une tangente à $\mathscr{C}$ passant par le point A(1;0)? Justifier.

On considère la fonction $f$ définie sur $\mathbb{R}\backslash{\{0\}}$ par \[ f(x)=\frac{(1-x)^3}{x^2}\].
Étudier les variations de la fonction $f$.

On considère la fonction $f$ définie sur $\mathbb{R}$ par $f(x)=\frac{(1-x)^3}{1+x^2}$. On note $\mathscr{C}$ la courbe représentative de $f$.
Peut-on trouver des points de $\mathscr{C}$ où la tangente à $\mathscr{C}$ est parallèle à la droite $\Delta$ d'équation $y=-x+4$?
Dans l'affirmative, préciser le nombre de ces points et leur abscisse.
Pour traiter le problème, on a obtenu à l'aide d'un logiciel de calcul formel, le résultat suivant que vous pouvez utiliser: $\text{Développer}\left(\frac{-3(1-x)^2(1+x^2)-2x(1-x)^3}{\left(1+x^2\right)^2}\right)\rightarrow \frac{-x^4+4x-3}{x^4+2x^2+1}$

On a tracé deux courbes $\mathscr{C}_1$ et $\mathscr{C}_2$.
L'une est la courbe d'une fonction $f$ dérivable sur $\mathbb{R}$. L'autre est la courbe de sa dérivée $f'$.

1) Associer à chaque courbe, la fonction qui lui correspond en justifiant.
2) A l'aide du graphique, déterminer une équation de la tangente à la courbe de $f$ au point d'abscisse 1.

Soit $f$ la fonction définie sur $\mathbb{R}$ par $f(x)=x^2$ et $g$ la fonction définie sur $\mathbb{R}\backslash\{0\}$ par $g(x)=\frac 1x$.
L'objectif de ce problème est de montrer que les courbes de $f$ et $g$ admettent une tangente commune
dont on donnera une équation. On notera $\mathscr{C}_f$ la courbe de $f$ et $\mathscr{C}_g$ la courbe de $g$.
1) Déterminer une équation de la tangente à $\mathscr{C}_f$ au point d'abscisse $a$.
2) Déterminer une équation de la tangente à $\mathscr{C}_g$ au point d'abscisse $b$.
3) Démontrer que l'existence d'une tangente commune revient à résoudre $\left\{ \begin{array}{r@{~}c@{~}l} 2\,a\, & = & -\frac 1 {b^2} \\ -\,a^2\, & = & \frac 2 b \end{array} \right.$
4) Justifier que l'équation $x^3=-8$ admet une unique solution sur $\mathbb{R}$. Donner la valeur de cette solution.
5) Conclure.

Soit $f$ la fonction définie sur $[0;+\infty[$ par $f(x)=\sqrt{x}$. On note $\mathscr{C}_f$ la courbe de $f$.
Soit M un point de $\mathscr{C}_f$ et A le point de coordonnées (2;0).

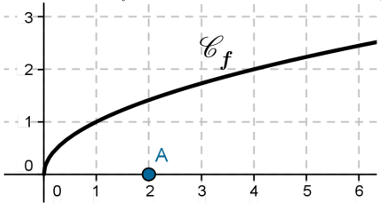
1) A l'aide du graphique ci-dessus, Déterminer graphiquement les coordonnées de M
     pour que la distance AM soit minimale.
2) On note $x$ l'abscisse de M et on pose $g(x)=AM$.
     a) Montrer que pour tout $x\ge 0$, $g(x)=\sqrt{x^2-3x+4}$.
     b) Justifier que $g$ est définie et dérivable sur $[0;+\infty[$ et déterminer $g'(x)$.
     c) En déduire les variations de $g$.
     d) Refaire la question 1) par le calcul.
3) On suppose maintenant que le point M a pour abscisse $\frac 32$.
     a) On appelle T la tangente à $\mathscr{C}_f$ en M. Déterminer le coefficient directeur de T.
     b) Tracer T sur le graphique où est tracée $\mathscr{C}_f$.
     c) Quelle conjecture peut-on faire concernant T et la droite (AM)?
     d) Démontrer cette conjecture.