produit scalaire dans l'espace

Définition

♦ Comprendre la définition expliquée en vidéo

Définition: Pour calculer le produit scalaire de 2 vecteurs $\vec u$ et $\vec v$:
1) On trouve 3 points A, B, C tels que $\overrightarrow{\mathrm{AB}}=\vec u$ et $\overrightarrow{\mathrm{AC}}=\vec v$.
2) Par définition, le produit scalaire $\vec u \cdot \vec v$ dans l'espace est égal au produit scalaire $\overrightarrow{\mathrm{AB}}\cdot \overrightarrow{\mathrm{AC}}$ dans le plan.
Calculer un produit scalaire dans l'espace revient à

calculer un produit scalaire dans le plan
car les 3 points A, B et C sont toujours dans un plan.
Le produit scalaire ne dépend pas

du choix des 3 points.
Le résultat d'un produit scalaire est toujours

un nombre.
Scalaire veut dire nombre, par opposition à vecteur.

♦ 6 techniques pour calculer un produit scalaire dans l'espace

Utiliser la définition

Pour calculer le produit scalaire $\vec u\cdot \vec v$:
Penser à choisir deux représentants de $\vec u$ et $\vec v$ qui soient dans un même plan.
Si on connait des longueurs

Si on connait les longueurs des 3 côtés du triangle ABC:
\[\overrightarrow{\mathrm{AB}}\cdot \overrightarrow{\mathrm{AC}}=\frac 12(\mathrm{AB}^2+\mathrm{AC}^2-\mathrm{BC}^2)\]

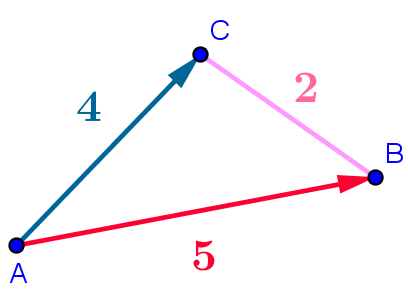
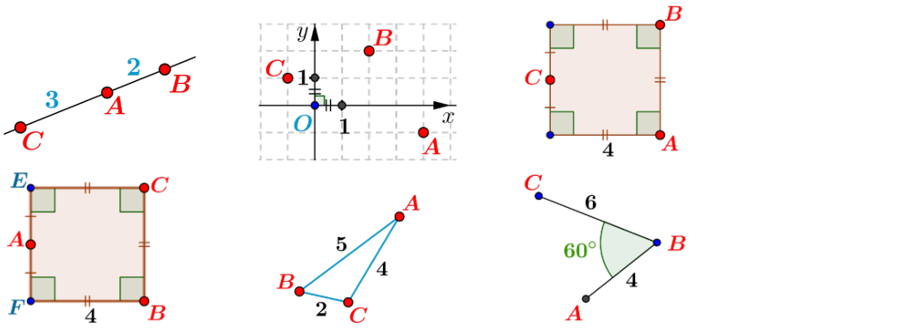
\[\overrightarrow{\mathrm{AB}}\cdot \overrightarrow{\mathrm{AC}}=\frac 12(25+16-4)=\frac{37}2\]

Cela vient de la propriété:
\[\vec u \cdot\vec v=\frac12(||\vec u||^2+||\vec v||^2-||\vec u-\vec v||^2)\]

Si on connait un angle

\[\overrightarrow{\mathrm{AB}}\cdot \overrightarrow{\mathrm{AC}}=\mathrm{AB}\cdot\mathrm{AC}\cdot\cos(\alpha)\]

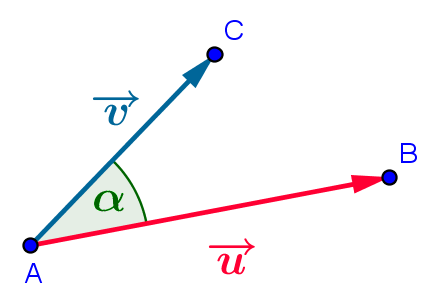Cas particuliers:

Si $\overrightarrow{\mathrm{AB}}$ et $\overrightarrow{\mathrm{AC}}$ sont colinéaires et de même sens :	\[\overrightarrow{\mathrm{AB}}\cdot \overrightarrow{\mathrm{AC}}=\mathrm{AB}\cdot\mathrm{AC}\]	car alors $\alpha=0$ et donc $\cos(\alpha)=1$
Si $\overrightarrow{\mathrm{AB}}$ et $\overrightarrow{\mathrm{AC}}$ sont colinéaires et de sens contraires :	\[\overrightarrow{\mathrm{AB}}\cdot \overrightarrow{\mathrm{AC}}=-\mathrm{AB}\cdot\mathrm{AC}\]	car alors $\alpha=\pi$ et donc $\cos(\alpha)=-1$

Avec un projeté orthogonal

2 façons de projeter:

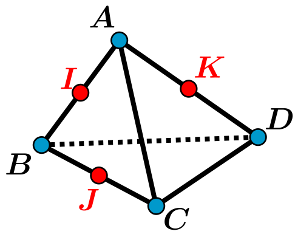
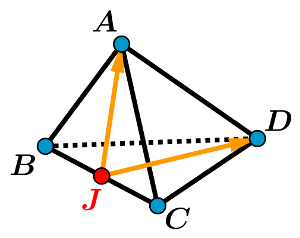
• Projeter C sur la droite (AB)	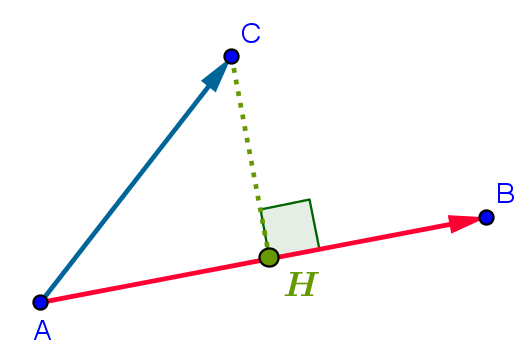\[\overrightarrow{\mathrm{AB}}\cdot \overrightarrow{\mathrm{AC}}=\overrightarrow{\mathrm{AB}}\cdot \overrightarrow{\mathrm{AH}}\] Pour conclure, utiliser le fait que: $\overrightarrow{\mathrm{AB}}$ et $\overrightarrow{\mathrm{AH}}$ sont colinéaires
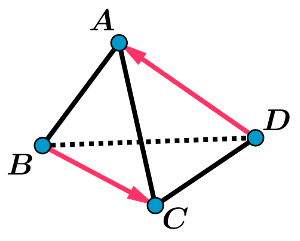
• Projeter B sur la droite (AC)	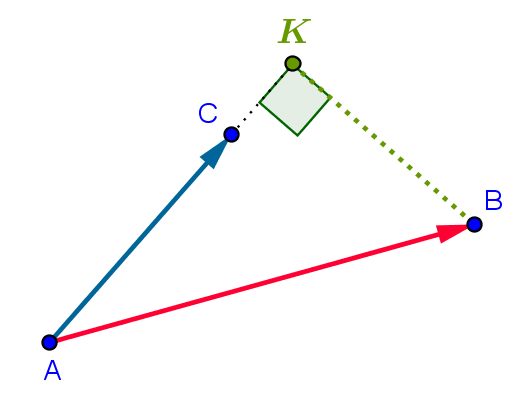\[\overrightarrow{\mathrm{AB}}\cdot \overrightarrow{\mathrm{AC}}=\overrightarrow{\mathrm{AC}}\cdot \overrightarrow{\mathrm{AK}}\] Pour conclure, utiliser le fait que: $\overrightarrow{\mathrm{AC}}$ et $\overrightarrow{\mathrm{AK}}$ sont colinéaires

Avec une décomposition

Décomposer les vecteurs en utilisant des angles droits

\[\overrightarrow{\mathrm{JB}}\cdot \overrightarrow{\mathrm{JC}}=(\overrightarrow{\mathrm{JA}}+ \overrightarrow{\mathrm{AB}})(\overrightarrow{\mathrm{JD}}+ \overrightarrow{\mathrm{DC}})\]

puis développer
Avec les coordonnées

Si on est dans un repère orthonormé:
$\vec u\cdot \vec v=xx'+yy'+zz'$

où $\vec u\begin{pmatrix} x \\ y \\ z \end{pmatrix}$ et $\vec v\begin{pmatrix} x' \\ y' \\ z' \end{pmatrix}$

S'il n'y a pas de repère, penser à en choisir un orthonormé

Avec un cube, on peut choisir le repère orthonormé ($A;\overrightarrow{\mathrm{AB}};\overrightarrow{\mathrm{AD}};\overrightarrow{\mathrm{AE}}$)

Propriétés du produit scalaire

$\vec u\cdot\vec v=$

$\vec u\cdot\vec v=\vec v\cdot\vec u$

On dit que le produit scalaire est commutatif
$\vec u\cdot(\vec v+\vec w)=$

$\vec u\cdot(\vec v+\vec w)=\vec u\cdot\vec v+\vec u\cdot\vec w$

On dit que le produit scalaire est distributif par rapport à l'addition
$(\lambda\vec u)\cdot\vec v=$

$(\lambda\vec u)\cdot\vec v=\vec u\cdot (\lambda\vec v)=\lambda (\vec u\cdot\vec v)$
$||\vec u||^2=$

$||\vec u||^2=\vec u\cdot \vec u$

Par exemple: $||\vec u+\vec v||^2=(\vec u+\vec v)(\vec u+\vec v)$ puis développer.
$\vec u\cdot \vec u=$

$\vec u\cdot \vec u=||\vec u||^2$

Par exemple: $\overrightarrow{\mathrm{AB}}\cdot\overrightarrow{\mathrm{AB}}=\mathrm{AB}^2$.

Déterminer un
angle à l'aide du produit scalaire

Pour déterminer l'angle $\widehat{BAC}$

1) On calcule $\overrightarrow{\mathrm{AB}}\cdot\overrightarrow{\mathrm{AC}}$ .
2) On trouve le cosinus grâce à : \[\cos\widehat{BAC}=\frac{\overrightarrow{\mathrm{AB}}\cdot\overrightarrow{\mathrm{AC}}}{\mathrm{AB}\times\mathrm{AC}}\].
3) Puis connaissant le cosinus, on trouve l'angle.

Corrigé en vidéo

Exercices 1 - Rappel: Comment

calculer un produit scalaire dans le plan

: les 6 techniques

Calculer le produit scalaire $\overrightarrow{\mathrm{AB}}\cdot\overrightarrow{\mathrm{AC}}$ dans chacun des cas suivants:

Corrigé en vidéo

Exercices 2 -

calculer un produit scalaire dans l'espace

avec et sans repère

ABCDEFGH est un cube d'arête 1.
Calculer le produit scalaire $\overrightarrow{\mathrm{DF}}\cdot\overrightarrow{\mathrm{BG}}$:
1) sans utiliser de repère.
2) à l'aide d'un repère.

Corrigé en vidéo

Exercices 3 -

produit scalaire dans l'espace avec un tétraèdre

ABCD est un tétraèdre régulier d'arête $a$.
I, J et K sont les milieux respectifs de [AB], [BC] et [AD].
Déterminer les produits scalaires suivants:
     1) $\overrightarrow{\mathrm{AC}}\cdot\overrightarrow{\mathrm{AD}}$
     2) $\overrightarrow{\mathrm{BI}}\cdot\overrightarrow{\mathrm{AJ}}$
     3) $\overrightarrow{\mathrm{IJ}}\cdot\overrightarrow{\mathrm{CD}}$
     4) $\overrightarrow{\mathrm{JK}}\cdot\overrightarrow{\mathrm{AD}}$

Corrigé en vidéo

Exercices 4 -

produit scalaire dans l'espace avec un tétraèdre

ABCD est un tétraèdre régulier d'arête $a$.
J est le milieu de [BC].
Déterminer le produit scalaire $\overrightarrow{\mathrm{JA}}\cdot\overrightarrow{\mathrm{JD}}$

Corrigé en vidéo

Exercices 5 -

produit scalaire dans l'espace avec un tétraèdre

ABCD est un tétraèdre régulier d'arête $a$.
Déterminer le produit scalaire $\overrightarrow{\mathrm{BC}}\cdot\overrightarrow{\mathrm{DA}}$

Corrigé en vidéo

Exercices 6 -

produit scalaire dans l'espace avec une pyramide

ABCDE est une pyramide à base carrée de sommet E.
Toutes les arêtes sont de même longueur $a$.
Déterminer les produits scalaires suivants:
$\overrightarrow{\mathrm{EA}}\cdot\overrightarrow{\mathrm{EB}}$ $\overrightarrow{\mathrm{EA}}\cdot\overrightarrow{\mathrm{EC}}$ $\overrightarrow{\mathrm{EA}}\cdot\overrightarrow{\mathrm{DC}}$ $\overrightarrow{\mathrm{ED}}\cdot\overrightarrow{\mathrm{DB}}$ $\overrightarrow{\mathrm{DB}}\cdot\overrightarrow{\mathrm{EC}}$

Corrigé en vidéo

Exercices 7 -

calculer un angle avec un produit scalaire

ABCDEFGH est un cube d'arête de longueur 1.
I et J sont les milieux respectifs de [AE] et [BC].
Déterminer la mesure de l'angle $\widehat{HIJ}$ à un degré près.

Exercices 8 - calculer

un angle avec un produit scalaire

ABCD est un tétraèdre régulier de côté $a$.
J est le milieu de [BC].
Déterminer une mesure de l'angle $\widehat{AJD}$ à 0.1° près.

Corrigé en vidéo!

Exercices 9 -

angle maximum

dans l'espace - produit scalaire - Bac S Liban 2017

On considère un cube $\rm ABCDEFGH$ dont la représentation graphique en perspective cavalière est donnée ci-dessous.

Les arêtes sont de longueur 1. L’espace est rapporté au repère orthonormé $\rm \left(D;\overrightarrow{DA};\overrightarrow{DC};\overrightarrow{DH}\right)$.
À tout réel $x$ de l’intervalle $[0;1]$, on associe le point $\rm M$ du segment $\rm [DF]$ tel que $\overrightarrow{\rm DM}=x \overrightarrow{\rm DF}$.
On s’intéresse à l’évolution de la mesure $\theta$ en radian de l’angle $\rm \widehat{EMB}$ lorsque le point $\rm M$ parcourt le segment $\rm [DF]$. On a $0\le \theta \le \pi$.
1) Que vaut $\theta$ si le point $\rm M$ est confondu avec le point $\rm D$? avec le point $\rm F$?
2) Justifier que les coordonnées du point $\rm M$ sont $(x ; x ; x)$.
3) Montrer que $\cos(\theta) =\frac{ 3x^2 -4x +1}{3x^2-4x+2}$.
4) On a construit ci-dessous le tableau de variations de la fonction $f: x\mapsto \frac{ 3x^2 -4x +1}{3x^2-4x+2}$.

     Pour quelles positions du point $\rm M$ sur le segment $\rm [DF]$ :
     a) le triangle $\rm MEB$ est-il rectangle en $\rm M$ ?
     b) l’angle $\theta$ est-il maximal?

Si \(\overrightarrow{\mathrm{AB}}\) et \(\overrightarrow{\mathrm{AC}}\) sont colinéaires et de même sens :	\[\overrightarrow{\mathrm{AB}}\cdot \overrightarrow{\mathrm{AC}}=\mathrm{AB}\cdot\mathrm{AC}\]	car alors \(\alpha=0\) et donc \(\cos(\alpha)=1\)
Si \(\overrightarrow{\mathrm{AB}}\) et \(\overrightarrow{\mathrm{AC}}\) sont colinéaires et de sens contraires :	\[\overrightarrow{\mathrm{AB}}\cdot \overrightarrow{\mathrm{AC}}=-\mathrm{AB}\cdot\mathrm{AC}\]	car alors \(\alpha=\pi\) et donc \(\cos(\alpha)=-1\)

Produit scalaire dans l'espace

Définition

Propriétés du produit scalaire

angle à l'aide du produit scalaire

calculer un produit scalaire dans le plan

calculer un produit scalaire dans l'espace

produit scalaire dans l'espace avec un tétraèdre

produit scalaire dans l'espace avec un tétraèdre

produit scalaire dans l'espace avec un tétraèdre

produit scalaire dans l'espace avec une pyramide

calculer un angle avec un produit scalaire

un angle avec un produit scalaire

angle maximum