Corrigé en vidéo!
Exercices 1:
Simplifier une expression avec la fonction exponentielle
Simplifier les expressions suivantes où \(x\) est un réel quelconque:
\[a)~\frac{e^{1+x}}{e^{x+2}}\]
\[b)~\frac{e^{3x}+e^x}{e^{2x}+e^x}\]
\[c)~\left(\frac{e}{e^{-x}}\right)^4\]


Corrigé en vidéo!
Exercices 2: Résoudre des
équations avec la fonction exponentielle
Résoudre dans \(\mathbb{R}\) les équations suivantes:
| \[a)~e^{2-x}=e^x\] |
\[b)~e^{2x+3}=1\] |
\[c)~e^{5-x^2}=e\] |
| \[d)~e^{-x}=0\] |
\[e)~2e^{-x}=\frac{4}{e^x+1}\] |
\[f)~2e^{-x}=\frac{1}{e^x+1}\] |


Corrigé en vidéo!
Exercices 3:
Inéquation et fonction exponentielle
Résoudre dans \(\mathbb{R}\) l'inéquation suivante:
\[1-e^{x^2-1}>0\]


Corrigé en vidéo!
Exercices 4: Résoudre des
inéquations avec la fonction exponentielle
Résoudre dans \(\mathbb{R}\) les inéquations suivantes:
\[a)~e^{2x}-e^{x+1}<0\] |
\[b)~1-e^{x-2}\ge 0\] |
\[c)~e^x-\frac{1}{e^x} \le 0\] |
\[d)~\frac {1}{e^x}-e>0\] |


Exercices 5: Résoudre des équations et inéquations avec des exponentielles en posant
X=e^x - changement d'inconnue.
Résoudre dans \(\mathbb{R}\) les équations et inéquations suivantes, en posant \(X=e^x\):
\[a)~2e^{2x}-e^x=1\]
\[b)~e^{2x}+2e^x-3\le 0\]


Corrigé en vidéo!
Exercices 6: Déterminer le
signe d'une expression avec la fonction exponentielle
Déterminer le signe des expressions suivantes sur \(\mathbb{R}\):
\[a)~1-e^x\]
\[b)~e^{2x}-1\]
\[c)~e^{2x}-e^{x+1}\]
\[d)~e^{(x^2)}-e^{x}\]
\[e)~1-\frac 1{e^{x}}\]


Corrigé en vidéo!
Exercices 7:
Inégalité avec la fonction exponentielle
Soit $f$ la fonction définie sur $\mathbb{R}$ par $f(x)=1-e^{-x}$.
1) Démontrer que pour tout réel $x<0$, \[f(x)<0\].
2) Démontrer que pour tout réel $x\ge 0$, \[0\le f(x)<1\] .


Corrigé en vidéo!
Exercice 8:
Fonction exponentielle et inégalité
Démontrer que pour tout $x\in ]-\infty;0[$, $e^{5x}-3\lt 0$.


Corrigé en vidéo!
Exercice 9: Déterminer des
limites avec la fonction exponentielle
Étudier les limites suivantes:
\[a)~\lim_{\substack{x \to +\infty}} x-e^x+1\]
\[b)~\lim_{\substack{x \to -\infty}} x-e^x+1\]
\[c)~\lim_{\substack{x \to +\infty}} \frac{e^x-x}{e^{2x}+1}\]
\[d)~\lim_{\substack{x \to +\infty}} xe^x-x-1\]


Corrigé en vidéo!
Exercice 10: limite avec des exponentielles
Étudier les limites suivantes:
\[a)~\lim_{\substack{x \to +\infty}} \left(2x+1\right){e^{-x}}\]
\[b)~\lim_{\substack{x \to -\infty}} \frac{2x+1}{e^{x}}\]
\[c)~\lim_{\substack{x \to -\infty}} {x}\left(e^{2x}-e^x\right)\]


Corrigé en vidéo!
Exercice 11: limite avec des exponentielles
Étudier les limites suivantes:
\[a)~\lim_{\substack{x \to +\infty}} {e^{-0.5x}}\]
\[b)~\lim_{\substack{x \to +\infty}} \frac{e^{0.1x}}{x}\]
\[c)~\lim_{\substack{x \to +\infty}} xe^{1-x}\]
\[d)~\lim_{\substack{x \to -\infty}} xe^{1-x}\]


Corrigé en vidéo!
Exercice 12:
Fonction exponentielle - limite
Déterminer $\lim\limits_{\substack{x \to -\infty}}xe^{4x}$.


Corrigé en vidéo!
Exercice 13:
limite d'une composée
avec la fonction exponentielle
Étudier les limites suivantes:
\[a)~\lim_{x \to +\infty} e^{1-x}\]
\[b)~\lim_{\substack{x \to 0\\x<0}} e^{\frac 1x}\]
\[c)~\lim_{\substack{x \to 0\\x>0}} e^{\frac 1x}\]
\[d)~\lim_{x \to -\infty} e^{\frac 1x}\]


Exercice 14:
Étudier les limites suivantes:
\[a)~\lim_{\substack{x \to +\infty}} {x e^{-\frac x2}}\]
\[b)~\lim_{\substack{x \to -\infty}} {x e^{-\frac x2}}\]


Corrigé en vidéo!
Exercice 15:
limite d'une composée
avec des exponentielles
Étudier les limites suivantes:
\[a)~\lim_{\substack{x \to -\infty}} e^{x^2-x+1}\]
\[b)~\lim_{\substack{x \to -\infty}} e^{x^3-x}\]


Exercice 16:
limite d'une composée
avec la fonction exponentielle
Étudier les limites suivantes:
\[a)~\lim_{x \to +\infty} xe^{\frac{1}{2x}}\]
\[b)~\lim_{x \to -\infty} xe^{\frac{1}{2x}}\]
\[c)~\lim_{\substack{x \to 0\\x>0}} xe^{\frac{1}{2x}}\]
\[b)~\lim_{\substack{x \to 0\\x<0}} xe^{\frac{1}{2x}}\]


Corrigé en vidéo!
Exercice 17: Déterminer la
dérivée et le tableau de variations avec la fonction
exponentielle
On considère la fonction \(f\) définie sur \(\mathbb{R}\) par \[f(x)=e^{1-3x}\].
1) Déterminer \(f'(x)\) pour tout \(x\) de \(\mathbb{R}\) puis en déduire le tableau de variations de \(f\)
sur \(\mathbb{R}\).
2) Déterminer le tableau de variations de \(f\) sur \(\mathbb{R}\) sans utiliser la dérivation.


Corrigé en vidéo!
Exercice 18: variations et exponentielle
On considère la fonction $f$ définie sur $\mathbb{R}$ par $f(x)=x^2e^{-x}$.
Déterminer $f'(x)$ pour tout $x$ de $\mathbb{R}$ puis en déduire le tableau de variations de $f$ sur
$\mathbb{R}$.


Corrigé en vidéo!
Exercice 19: Déterminer la
dérivée et le tableau de variations avec la fonction
exponentielle
Déterminer le tableau de variations de \(f\) définie sur sur $\mathbb{R}\backslash\{0\}$ par
$f(x)=xe^{^{\frac 1x}}$


Corrigé en vidéo!
Exercice 20: Déterminer la
dérivée et le tableau de variations avec la fonction
exponentielle
, et cosinus
On considère la fonction \(f\) définie sur \([0;2\pi]\) par \(f(x)=e^{\cos x}\).
1) Déterminer pour tout \(x\) de \([0;2\pi]\), \(f'(x)\).
2) En déduire le tableau de variations de \(f\) sur \([0;2\pi]\).


Exercice 21: Associer courbe et fonction exponentielle
On a tracé les courbes de quatre fonctions $f, g, h, i$ définies sur $\mathbb{R}$.
On sait que $f(x)=e^{x}$, $g(x)=e^{-x}$, $h(x)=e^{0.5x}$, $i(x)=e^{-2x}$
Associer à chaque fonction la courbe qui lui correspond en
justifiant.


Exercice 22:
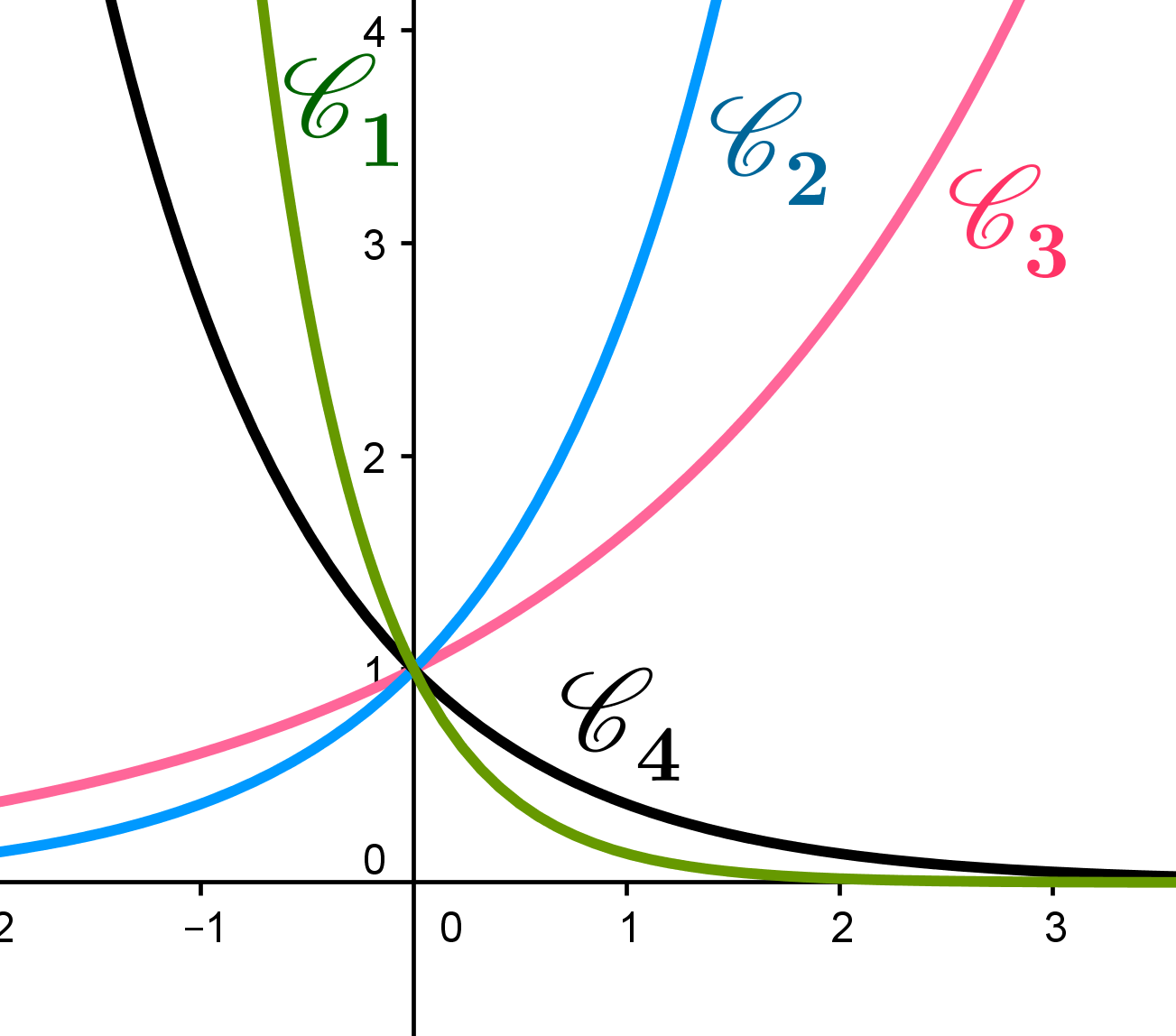
On a tracé les courbes de cinq fonctions \(f, g, h, i, j\) définies sur \(\mathbb{R}\).

Les droites d'équation \(y=-1\) et \(y=1\) sont asymptotes en \(+\infty\) respectivement à \(\mathscr{C}_2\)
et \(\mathscr{C}_3\).
On sait que \(f(x)=e^{-x}-1\), \(g(x)=-2e^x+2\), \(h(x)=e^x-1\),
\[i(x)=\frac{e^x+e^{-x}}2-1\] et
\[j(x)=\frac{e^x-1}{e^x+1}\]
Associer à chaque fonction la courbe qui lui correspond en justifiant.


Exercice 23: Déterminer a, b dans f(x)=(ax+b)e^(-x)
On a tracé la courbe \(\mathscr{C}_f\) d'une fonction \(f\) définie sur \(\mathbb{R}\).
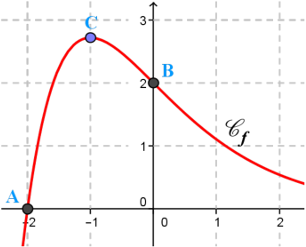
La courbe de \(f\) passe par les points \(A(-2;0)\), \(B(0;2)\).
On sait que pour tout \(x\) réel:
\(f(x)=(ax+b)e^{-x}\) où \(a\) et \(b\) sont des réels.
1) A l'aide du graphique, déterminer \(a\) et \(b\) en justifiant.
2) En déduire le tableau de variations de \(f\).


Corrigé en vidéo!
Exercice 24:
Déterminer a, b,c dans f(x)=(ax²+bx+c)e^(-x)
On a tracé la courbe \(\mathscr{C}_f\) d'une fonction \(f\) définie sur \(\mathbb{R}\).
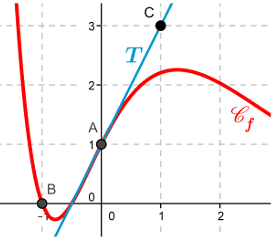
\(\mathscr{C}_f\) passe par les points A(0;1) et B(-1;0).
\(T\) est la tangente à \(\mathscr{C}_f\) en A et passe par le point C(1;3).
On sait également que pour tout \(x\) réel:
\(f(x)=(ax^2+bx+c)e^{-x}\) où \(a\), \(b\), \(c\) sont des nombres.
1) Déterminer, pour tout \(x\) réel, \(f'(x)\).
2) Déterminer la valeur de \(a\), \(b\) et \(c\) en justifiant.


Corrigé en vidéo!
Exercice 25: Tableau de
variation de e^u
connaissant celui de u -
Limite
d'une composée avec la fonction exponentielle
Une fonction \(u\) définie sur \(\mathbb{R}\) a pour tableau de variations:
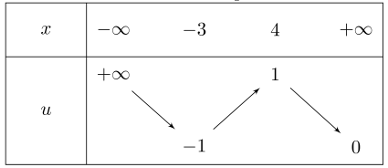
1) Déterminer le tableau de variations de la fonction \(e^u\).
2) Déterminer les limites de \(e^u\) en \(-\infty\) et \(+\infty\).


Corrigé en vidéo!
Exercice 26:
Tangentes perpendiculaires et fonction exponentielle
On considère les fonctions \(f\) et \(g\) définies sur \(\mathbb{R}\) par \(f(x)=e^x\) et
\(g(x)=e^{-x}\).
Dans un repère orthonormé, on a tracé les courbes \(\mathscr{C}_f\) et \(\mathscr{C}_g\) de ces deux
fonctions.
1) Démontrer que si \(m\) est le coefficient directeur d'une droite \(\mathscr{D}\) du plan alors le
vecteur
de coordonnées \((1;m)\) est un vecteur directeur de cette droite.
2) Déterminer, pour tout \(x\) réel, \(f'(x)\) et \(g'(x)\).
3) On note \(T_a\) et \(\Delta_a\) les tangentes respectives à \(\mathscr{C}_f\) et
\(\mathscr{C}_g\)
au point d'abscisse \(a\).
a) Démontrer que les tangentes à \(\mathscr{C}_f\) et \(\mathscr{C}_g\)
au point d'abscisse 0 sont perpendiculaires.
b) Démontrer que les tangentes à \(\mathscr{C}_f\) et \(\mathscr{C}_g\) au point
d'abscisse \(a\)
sont perpendiculaires quel que soit \(a\) réel.
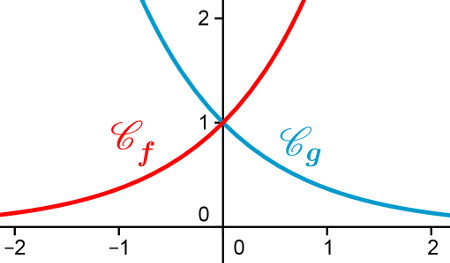


Corrigé en vidéo!
Exercice 27: Suite et fonction exponentielle
On considère la suite \((u_n)\) définie pour tout entier naturel \(n\) par \[u_n=4-e^{-\frac n2}\].
Démontrer que la suite \((u_n)\) est strictement croissante par 2 méthodes différentes.


Corrigé en vidéo!
Exercice 28: Somme de suite géométrique et fonction exponentielle
On considère la suite \((u_n)\) définie pour tout entier naturel \(n\) par \[u_n=e^{^{2-\frac n3}}\].
Pour tout entier naturel \(n\), on pose \({\rm S}_n=u_0+u_1+...+u_n\).
a) Démontrer que la suite \((u_n)\) est géométrique et préciser sa raison.
b) Exprimer la somme \({\rm S}_n\) en fonction de \(n\).
c) En déduire la limite de ${\rm S}_n$ quand $n$ tend vers $+\infty$.


Corrigé en vidéo!
Exercice 29: Somme de suite arithmétique et fonction exponentielle
On considère la suite $(u_n)$ définie pour tout entier naturel $n$ par $u_n=e^{2-\frac n3}$.
Pour tout entier naturel $n$, on pose ${\rm P}_n=u_0\times ...\times u_n$.
1) Exprimer le produit ${\rm P}_n$ en fonction de $n$.
2) Déterminer la limite de ${\rm P}_n$ quand $n$ tend vers $+\infty$.


Corrigé en vidéo!
Exercice 30: Nombre de solution d'une équation avec des exponentielles - Théorème des
valeurs intermédiaires
Déterminer le nombre de solution de l'équation \[\frac{e^x}{e^x+1}=x\].
Donner un encadrement d'amplitude \(10^{-1}\) des éventuelles solutions.


Exercice 31: Associer f et f ' à leur courbe - Déterminer a, b, c à l'aide de la
courbe de f et f'
On a récupéré un graphique avec deux courbes. $\mathscr{C}_f$ est la courbe d'une fonction $f$ et
$\mathscr{C}_{f'}$ de sa dérivée.
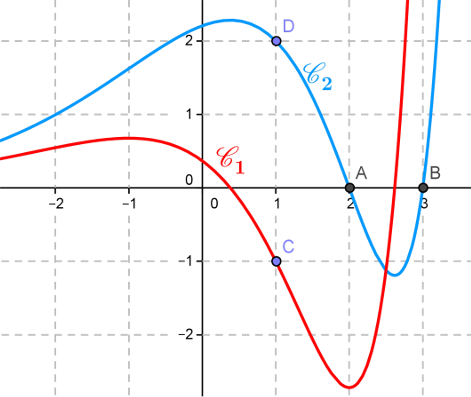
On sait que la fonction $f$ est définie par $f(x)=(x^2+ax+b)e^{x+c}$ où $a$, $b$ et $c$ sont des constantes
réelles.
L'objectif de cet exercice est retrouver les valeurs $a$, $b$ et $c$.
1) Justifier que $a$ et $b$ sont solutions du système:
$\left\{\begin{array}{l}
4+2a+b=0\\
9+3a+b=0 \\
\end{array}\right.$
2) En déduire les valeurs de $a$ et $b$.
3) Déterminer $f'(x)$.
4) A l'aide du point C, déterminer la valeur de $c$ et donner l'expression de $f(x)$.


Corrigé en vidéo!
Exercice 32: Suite récurrente et fonction exponentielle - u(n+1)=f(u(n)) -
u(n+1)=-une^(-un)
On considère la fonction $f$ définie sur $\mathbb{R}$ par $f(x)=x e^{-x}$ et $\mathscr{C}_f$ sa courbe
représentative ci-dessous:
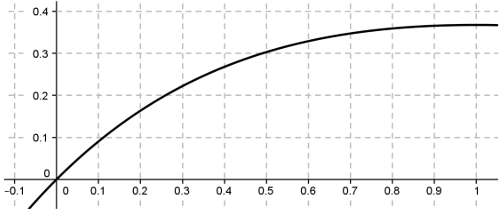
On note $(u_n)$ la suite définie pour tout entier naturel $n$ par $u_{n+1}=u_ne^{-u_n}$ et $u_0=1$.
1) Déterminer les variations de $f$.
2) Déterminer graphiquement $u_1$, $u_2$, $u_3$.
3) Conjecturer le sens de variation, un majorant et un minorant de la suite $(u_n)$.
4) Démontrer vos conjectures. En déduire que $(u_n)$ converge.
5) On note $\ell$ la limite de $(u_n)$. On admet que $\ell$ vérifie l'équation $\ell=\ell e^{-\ell}$.
Déterminer la valeur de $\ell$.


Corrigé en vidéo!
Exercice 33: fonction exponentielle - limite dérivation tableau de variation TVI -
bac mars 2019 Nouvelle Calédonie
Soient $g$ et $f$ les fonctions définies sur $\mathbb{R}$ par $g(x) = (x+2)\text{e}^{x-4}-2$ et $f(x)= x^2
-x^2\text{e}^{x-4}$.
- Déterminer les limites de $g$ en $+\infty$ et en $-\infty$.
- Dresser le tableau de variation de $g$. (On admet que $g$ est dérivable sur $\mathbb{R}$).
- Démontrer que l'équation $g(x)=0$ admet une solution unique $\alpha$ sur $\mathbb{R}$ et donner un
encadrement de $\alpha$ à $10^{-2}$.
- En déduire le signe de $g$ sur $\mathbb{R}$.
- Étudier les limites de $f$ en $-\infty$ et en $+\infty$.
- Montrer que pour tout $x$, $f'(x)=-xg(x)$. (On admet que $f$ est dérivable sur $\mathbb{R}$).
- En déduire les variations de $f$.
- Démontrer que le maximum de $f$ sur $[0~;~+\infty[$ est $\dfrac{\alpha^3}{\alpha+2}$.


Exercice 34:
Distance d'un point à la courbe de la fonction exponentielle
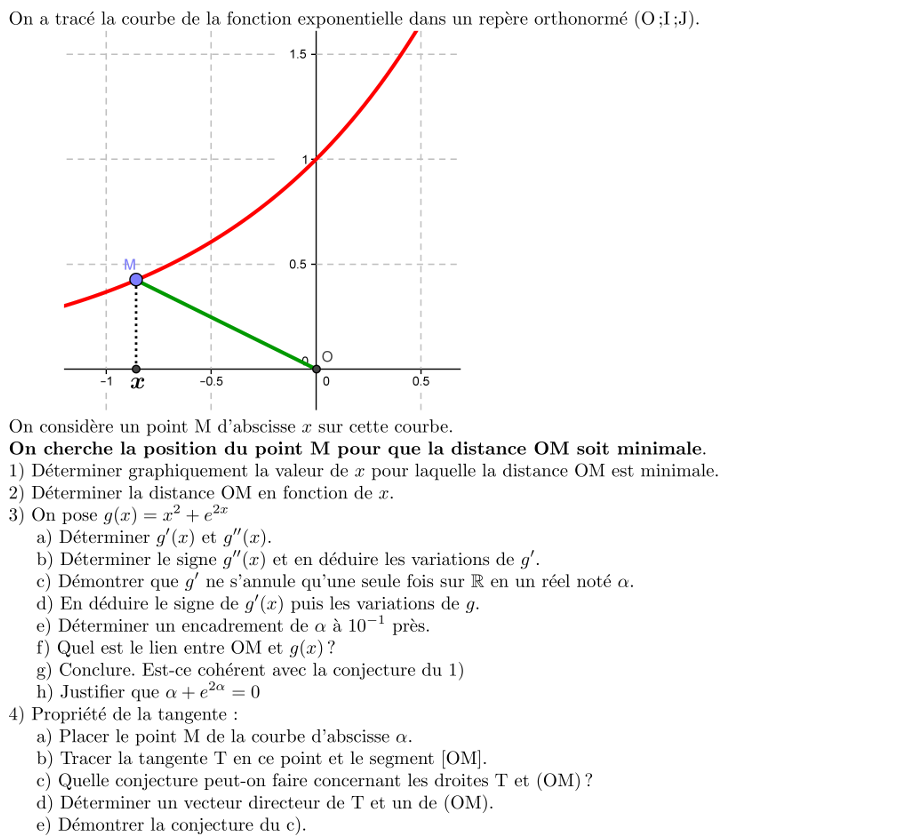


Corrigé en vidéo!
Exercice 35: Encadrement et
valeur approchée de e
-
suite
convergente vers e
-
(1+1/n)^n
L'objectif de cet exercice est de trouver une valeur approchée de e.
On considère la fonction \(f\) définie sur \(\mathbb{R}\) par \(f(x)=e^x-x-1\).
1) Étudier les variations de \(f\) et en déduire que pour tout \(x\) réel, \(~1+x\le e^x\).
2) En déduire que pour \(x<1\),
\[~e^x\le \frac1{1-x}\].
3) Déduire du 1) que pour tout entier \(n\ge 1\),
\[~\left(1+\frac 1n\right)^n\le
e\].
4) Déduire du 2) que pour tout entier \(n\ge 1\),
\[~e\le \left(1+\frac
1n\right)^{n+1}\].

Indication:
Pose
x =
1
/
n+1
5) En déduire un encadrement de \(e\) à \(10^{-2}\) près.
6) Soit la suite \((u_n)\) définie pour tout entier \(n\ge1\) par
\[~u_n=\left(1+\frac 1n\right)^n\].
Démontrer que pour tout entier \(n\ge1\),
\[~e-\frac
3n\le u_n \le e\]. En déduire la limite de \((u_n)\).


Corrigé en vidéo!
Exercice 36:
Pondichery Bac S 2013
- Les 2 questions sur la fonction
exponentielle qui ont déstabilisé certains candidats
La hauteur, en mètre, d'un plant de maïs à l'instant \(t\) est modélisée
par la fonction \(h\) définie sur \([0;+\infty[\) par \[h(t)=\frac
a{1+be^{-0.04t}}\]
où \(t\) est exprimé en jour. \(a\) et \(b\) sont des constantes réelles.
On sait qu'à l'instant \(t=0\), le plant mesure \(0,1\) m
et que sa hauteur tend vers \(2\) m.
1) Déterminer \(a\) et \(b\).
2) On a représenté la courbe de la fonction \(h\).
La vitesse de croissance du plant de maïs
correspond à la dérivée de la fonction \(h\).
A l'aide du graphique, déterminer une valeur approchée
de l'instant \(t\) où la vitesse de croissance est maximale.
A quelle hauteur du plant cela correspond-il?



Exercice 37:
Problème ouvert - Convexité et fonction exponentielle
Soit $\mathscr{C}$ la courbe de la fonction exponentielle et A et B deux points distincts de
$\mathscr{C}$.
Montrer que le segment [AB] est au dessus de la courbe $\mathscr{C}$.






 ♦ Comment obtenir la courbe de l'exponentielle: Méthode d'Euler
♦ Comment obtenir la courbe de l'exponentielle: Méthode d'Euler

 ♦ Comprendre la
définition mathématique
♦ Comprendre la
définition mathématique

 exp(-x) =
exp(-x) =
 exp(x-y) =
exp(x-y) =
















 $\lim\limits_{x \rightarrow -\infty} e^x=$
$\lim\limits_{x \rightarrow -\infty} e^x=$


 $\lim\limits_{x \rightarrow +\infty} \dfrac {e^x}{x^n}=$
$\lim\limits_{x \rightarrow +\infty} \dfrac {e^x}{x^n}=$
 $\lim\limits_{x \rightarrow -\infty} xe^x=$
$\lim\limits_{x \rightarrow -\infty} xe^x=$































 Exercice 14:
Exercice 14: 


 Exercice 16:
Exercice 16: 















 La courbe de \(f\) passe par les points \(A(-2;0)\), \(B(0;2)\).
La courbe de \(f\) passe par les points \(A(-2;0)\), \(B(0;2)\).

 \(\mathscr{C}_f\) passe par les points A(0;1) et B(-1;0).
\(\mathscr{C}_f\) passe par les points A(0;1) et B(-1;0).




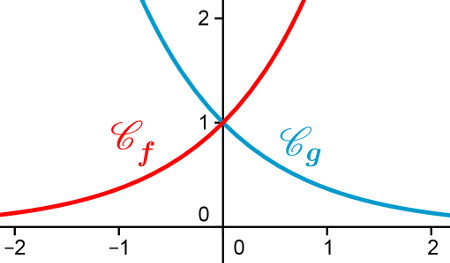









 Exercice 31: Associer f et f ' à leur courbe - Déterminer a, b, c à l'aide de la
courbe de f et f'
Exercice 31: Associer f et f ' à leur courbe - Déterminer a, b, c à l'aide de la
courbe de f et f'


















