Théorème de Gauss - Cours et exercices - arithmétique

Corrigé en vidéo

Exercices 1:

Equation diophantienne - Arithmétique - Spé Maths

Justifier que l'équation : $15x-9y = 14$ n'admet aucun couple d'entiers $(x~;~y)$ solution.
On souhaite maintenant résoudre dans $\mathbb{Z}^2$ l'équation $(E) : 13x + 9y = 2$.
1. Justifier que $(E)$ possède au moins un couple d'entiers solution.
2. Déterminer un couple $(x_0~;~y_0)$ d'entiers solution de $(E)$.
3. Montrer que l'équation $(E)$ est équivalente à $(E') : 13(x-x_0) = -9(y-y_0)$.
4. Montrer que si $(x~;~y)$ est un couple d'entiers solution de $(E)$ alors il existe un entier $k$ tel que : $x = -4 + 9k$ et $y= 6-13k$.
5. Déterminer l'ensemble des couples d'entiers solutions de l'équation $(E)$.

Corrigé en vidéo

Exercices 2:

Utilisation du corollaire du théorème de Gauss - Arithmétique - Nombre de Mersenne - Spé Maths

Un élève utilise sa calculatrice et obtient les résultats ci-dessous:

Au vue des résultats, il affirme que $3$ divise $2^{33}-1$ et $4$ divise $2^{33}-1$ et que $12$ ne divise pas $2^{33}-1$.
1) En quoi cette affirmation est-elle contradictoire?
2) Justifier que, en réalité, $4$ ne divise pas $2^{33}-1$.
3) Montrer que $3$ ne divise pas $2^{33}-1$.
4) Démontrer que 7 divise $2^{33}-1$.

Corrigé en vidéo

Exercices 3:

Démonstration du théorème de Gauss - Arithmétique - Spé Maths

L'objectif de l'exercice est de démontrer le théorème de Gauss :

Soient $a$, $b$ et $c$ trois entiers non nuls.
Si $a$ divise le produit $bc$ et si $a$ et $b$ sont premiers entre eux, alors $a$ divise $c$.

1) Rappeler le théorème de Bézout.
2) Montrer qu'il existe deux entiers $u$ et $v$ tels que $acu + bcv = c$.
3) En déduire que $a$ divise $c$.

Corrigé en vidéo

Exercices 4:

Problème de dénombrement et théorème de Gauss - Arithmétique - Spé Maths

Un joueur a totalisé $200$ points en lançant sur une cible $25$ fléchettes.
La cible possède $3$ zones qui rapportent respectivement $0$, $5$ et $12$ points.
1) Montrer que le nombre de fléchettes qui ont touché la zone à $12$ points est divisible par $5$.
2) En déduire la répartition des fléchettes dans les différentes zones.

Corrigé en vidéo

Exercices 5:

Exercice d'application du théorème de Gauss - critère d'Eisenstein - Arithmétique - Spé Maths

Soient $p$ et $q$ deux entiers premiers entre eux. On considère l'équation (E): $3x^3 + 4x^2 +2x -4 = 0$

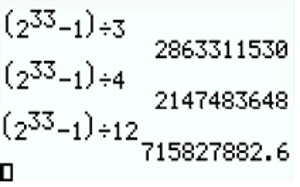
1)	Montrer que si $\frac{p}{q}$ est une solution de l'équation (E) alors $p$ divise $4$ et $q$ divise $3$.
2)	En déduire que l'équation $(E)$ admet une unique solution rationnelle.

Corrigé en vidéo

Exercices 6:

Théorème de Gauss: points à coordonnées entières sur une droite - Arithmétique - Spé Maths

Dans un repère orthonormé, on considère les points $A(7~;~2)$ et $B(-3~;~-4)$.
1) Montrer qu'un point $M(x~;~y)$ appartient à la droite $(AB)$ si et seulement si: $$3(x-7)=5(y-2)$$ 2) En déduire l'ensemble des points du plan à coordonnées entières appartenant à la droite $(AB)$.

Corrigé en vidéo

Exercices 7:

Corollaire du théorème de Gauss - Arithmétique - Spé Maths

L'objectif de l'exercice est de démontrer le corollaire du théorème de Gauss :

Soient $a$, $b$ et $n$ trois entiers non nuls.
Si $a$ et $b$ divisent $n$ et si $a$ et $b$ sont premiers entre eux, alors $ab$ divise $n$.

1) Montrer qu'il existe deux entiers $k$ et $k'$ tels que : $ka = k'b$.
2) Montrer que $a$ divise $k'$.
3) En déduire que $ab$ divise $n$.

Corrigé en vidéo

Exercices 8:

Exercice d'application du corollaire du théorème de Gauss - Arithmétique - Spé Maths

Montrer que le produit de $5$ entiers consécutifs est divisible par $120$.

Corrigé en vidéo

Exercices 9:

Problème des restes chinois - Arithmétique - Spé Maths


1)	On se propose de déterminer l'ensemble $\mathscr{S}$ des entiers relatifs $n$ vérifiant le système : \[\left\{\begin{array}{l c l} n &\equiv & 9 \quad [17]\\ n &\equiv &3 \quad [5] \end{array}\right.\]
	a)	On désigne par $(u~;~v)$ un couple d'entiers relatifs tel que $17u + 5v = 1$.
		(i)	Justifier l'existence d'un tel couple $(u~;~v)$.
		(ii)	On pose $n_{0} = 3 \times 17u + 9 \times 5v$. Démontrer que $n_{0}$ appartient à $\mathscr{S}$.
		(iii)	Donner un exemple d'entier $n_{0}$ appartenant à $\mathscr{S}$.
	b)	Soit $n$ un entier relatif appartenant à $\mathscr{S}$.
		(i)	Démontrer que $n - n_{0} \equiv 0\quad [85]$.
		(ii)	En déduire qu'un entier relatif $n$ appartient à $\mathscr{S}$ si et seulement si il peut s'écrire sous la forme $n = 43 + 85k$ où $k$ est un entier relatif.
2)	Zoé sait qu'elle a entre 300 et 400 jetons. Si elle fait des tas de 17 jetons, il lui en reste 9. Si elle fait des tas de 5 jetons, il lui en reste 3. Combien a-t-elle de jetons ?

Corrigé en vidéo

Exercices 10:

Exercice d'application du théorème de Gauss - Arithmétique - Spé Maths

Soient $a$ et $b$ deux rationnels (tous deux non nuls) tels que $a+b$ et $ab$ sont des entiers.
On pose $a = \dfrac{p_1}{q_1}$ avec $p_1$ et $q_1$ deux entiers premiers entre eux (avec $q_1 >0$) et
$b = \dfrac{p_2}{q_2}$ avec $p_2$ et $q_2$ deux entiers premiers entre eux (avec $q_2 >0$).
1) Montrer que $q_1$ divise $q_2$.
2) En déduire que $q_1=q_2$.
3) Prouver que $a$ et $b$ sont des entiers.

Corrigé en vidéo

Exercices 11:

Chiffrement affine - Montrer qu'une clé peut ne pas être satisfaisante

On numérote les 26 lettres de l'alphabet de 0 pour A à 25 pour Z.
On choisit 2 entiers naturels $a$ et $b$ avec $a\ne 0$. Le couple $(a;b)$ s'appelle la clé de chiffrement.
Pour coder la lettre numéro $x$, on calcule $f(x)=ax+b$. Comme le résultat peut ne pas être compris entre 0 et 25, on prend son reste dans la division euclidienne par 26. Puis ce nombre est remplacé par la lettre correspondante.
1) A quel chiffrement affine correspond ce tableau ci-dessous?

2) Rose propose d'utiliser la clé $(4;7)$. Cette clé, est-elle satisfaisante?

Corrigé en vidéo

Exercices 12:

Chiffrement affine - Montrer qu'une clé est satisfaisante

On numérote les 26 lettres de l'alphabet de 0 pour A à 25 pour Z.
On choisit 2 entiers naturels $a$ et $b$ avec $a\ne 0$. Le couple $(a;b)$ s'appelle la \textbf{clé} de chiffrement.
Pour coder la lettre numéro $x$, on calcule $f(x)=ax+b$. Comme le résultat peut ne pas être compris entre 0 et 25, on prend son reste dans la division euclidienne par 26. Puis ce nombre est remplacé par la lettre correspondante. Gaspard propose d'utiliser la clé $(3;9)$ pour coder un message.
1) Coder la lettre H.
2) Cette clé $(3;9)$ est-elle satisfaisante?

Corrigé en vidéo

Exercices 13:

Chiffrement affine - Cas général

On numérote les 26 lettres de l'alphabet de 0 pour A à 25 pour Z.
On choisit 2 entiers naturels $a$ et $b$ avec $a\ne 0$. Le couple $(a;b)$ s'appelle la clé de chiffrement.
Pour coder la lettre numéro $x$, on calcule $f(x)=ax+b$. Comme le résultat peut ne pas être compris entre 0 et 25, on prend son reste dans la division euclidienne par 26. Puis ce nombre est remplacé par la lettre correspondante. On dit qu'une clé est satisfaisante lorsque deux lettres différentes sont codées par deux lettres différentes.
1) Montrer que si $a$ et $26$ sont premiers entre eux alors la clé $(a;b)$ est satisfaisante.
2) Dans la suite du problème, on choisit une clé $(a;b)$ avec $a$ et $26$ premiers entre eux.
     a) Montrer qu'il existe un entier relatif $u$ tel que $au\equiv 1~[26]$.
     b) Déterminer une fonction de décodage.
     c) Décoder le message ZSPS qui a été codé avec la clé $(15;2)$.

Corrigé en vidéo

Exercices 14:

Théorème de Gauss - Erreur à éviter vue dans des copies

On considère l'équation $3(x-2)=10(y+5)$ où $x$ et $y$ sont des entiers. Un élève écrit:
Comme $\boldsymbol{3(x-2)=10(y+5)}$, donc 3 divise $\boldsymbol{10(y+5)}$.
Or 3 ne divise pas 10 donc 3 divise $\boldsymbol{y+5}$. Donc $\boldsymbol{y+5=3}k$ avec $\boldsymbol{k\in \mathbb{Z}}$.
1. Corriger l'erreur de l'élève.
2. Trouver un exemple pour convaincre l'élève que son raisonnement est faux.

Corrigé en vidéo

Exercices 15:

Equation diophantienne - Erreurs à éviter vue dans des copies

On considère l'équation ${(\rm E)}:~14(x-6)=9(y+2)$ où $x$ et $y$ sont des entiers. Un élève écrit:

     Comme $14(x-6)=9(y+2)$, donc $14$ divise $9(y+2)$.
     Or $14$ et $9$ sont premiers entre eux donc $14$ divise $y+2$.
     Donc $y+2=14k$ et donc $y=-2+14k$ avec $k\in \mathbb{Z}$.
     De même, $9$ divise $14(x-6)$. Or $9$ et $14$ sont premiers entre eux. Donc $9$ divise $x-6$.
     Donc $x-6=9k'$ c'est à dire $x=6+9k'$ avec $k\in \mathbb{Z}$.
     Les solutions de l'équation $({\rm E})$ sont $(6+9k';-2+14k)$ avec $k$ et $k'$ entiers.

Corriger les erreurs de l'élève.

Exercices 16:

Equation avec congruence - arithmétique - spé maths

$a$ et $n$ sont deux entiers naturels non nuls, et premiers entre eux.
Démontrer que l'équation d'inconnue $x$, $ax \equiv 2~[n]$ a au plus une solution dans $[0; n - 1]$.

Corrigé en vidéo

Exercices 17:

congruence - divisibilité - Théorème de Gauss - spécialité maths

Soit $n\in \mathbb{Z}$.
Montrer que 30 divise $n^5-n$

Corrigé en vidéo

Exercices 18:

Théorème de Gauss et nombre premier - spécialité maths

Dans tout l'exercice, $p$ est un nombre premier et $a$ et $b$ sont deux entiers naturels.

1. Justifier que si $p$ ne divise pas $a$, alors $p$ et $a$ sont premiers entre eux.
2. Montrer que si $p$ divise le produit $ab$ alors $p$ divise $a$ ou $p$ divise $b$.
Montrer que si $p$ divise $a^2$ alors $p$ divise $a$.
On suppose maintenant que $a$ et $b$ sont des nombres premiers.
Montrer que si $p$ divise le produit $ab$ alors $p=a$ ou $p=b$.

Corrigé en vidéo

Exercices 19:

nombre premier & nombre puissant BAC S 2018 métropole - Terminale S spécialité maths

Un entier naturel $n$ est appelé nombre puissant lorsque, pour tout diviseur premier $p$ de $n$, $p^2$ divise $n$.

Vérifier qu'il existe deux entiers consécutifs inférieurs à $10$ qui sont puissants.
Soient $a$ et $b$ deux entiers naturels. Montrer que l'entier naturel $n=a^2b^3$ est un nombre puissant.
Soit $x$ un entier naturel. Montrer que $8x^2$ et $x^2$ sont des entiers puissants.