























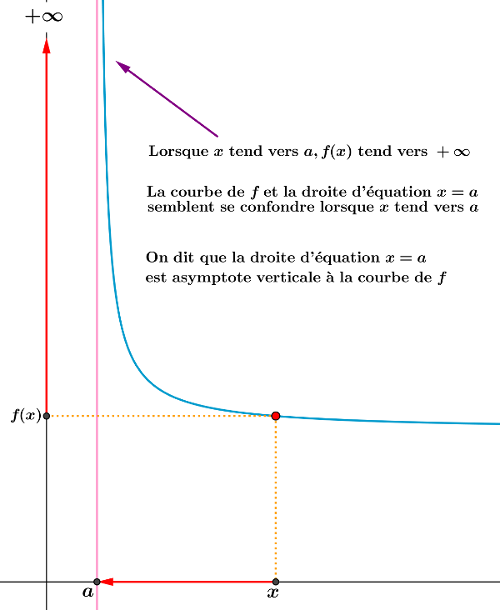


|
lim
x → +∞
x =

\[\lim_{x \to +\infty}x=+\infty\]
|
lim
x → -∞
x =

\[\lim_{x \to -\infty}x=-\infty\]
|
||
|
lim
x → +∞
1
x
=

\[\lim_{x \to +\infty}\frac 1x=0\]
|
lim
x → -∞
1
x
=

\[\lim_{x \to -\infty}\frac 1x=0\]
|
lim
x → 0
x>0
1
x
=

\[\lim_{\substack{x \to 0 \\ x\gt 0}}\frac
1x=+\infty\]
|
lim
x → 0
x<0
1
x
=

\[\lim_{\substack{x \to 0 \\ x\lt 0}}\frac
1x=-\infty\]
|
|
|
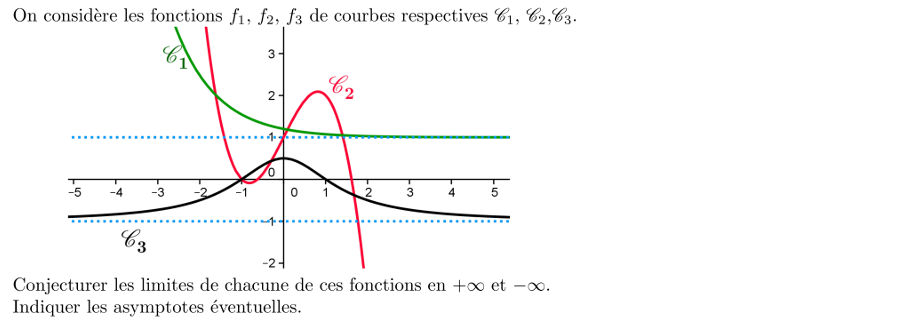

 Exercice
2:
Exercice
2: 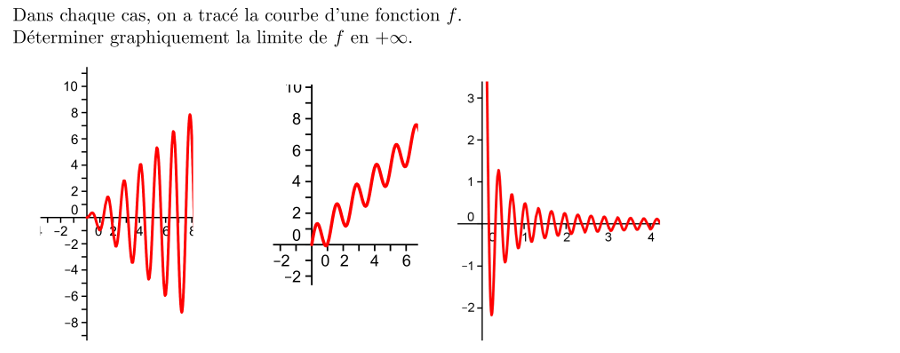


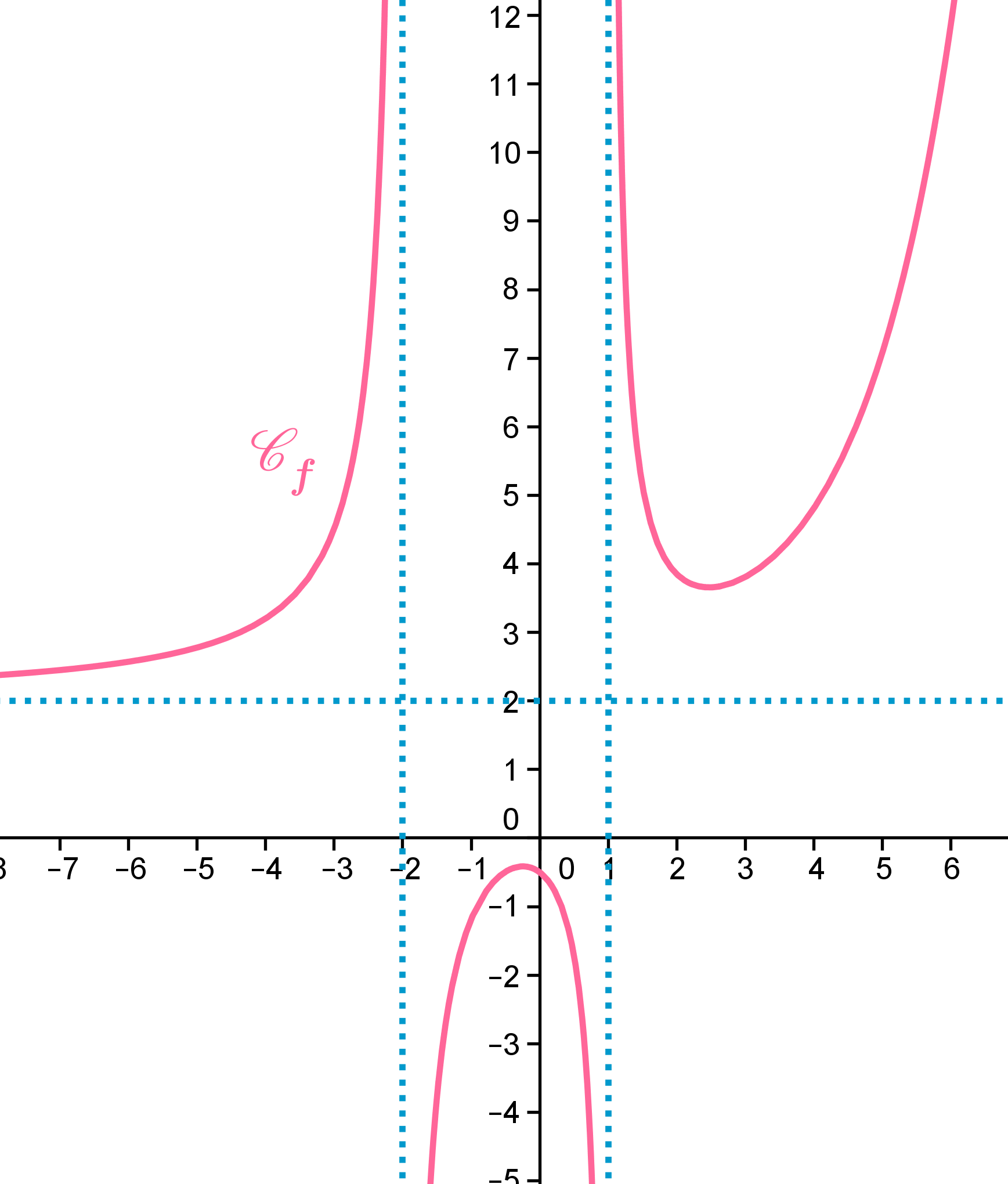

 Exercice
4: Tracer l'allure de la courbe d'une fonction connaissant les limites
Exercice
4: Tracer l'allure de la courbe d'une fonction connaissant les limites

 Exercice
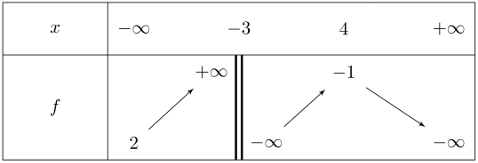
5: Lire les limites d'une fonction et asymptotes à partir du tableau de variations
Exercice
5: Lire les limites d'une fonction et asymptotes à partir du tableau de variations

 Exercice
6: Conjecturer une limite d'une fonction à l'aide de la calculatrice
Exercice
6: Conjecturer une limite d'une fonction à l'aide de la calculatrice

 Exercice
7: Déterminer les asymptotes à partir des limites
Exercice
7: Déterminer les asymptotes à partir des limites 




N'hesitez pas à envoyer un mail à:
jaicompris.com@gmail.com