Corrigé en vidéo
Exercice 1: Utiliser les tableaux pour trouver la
limite d'une fonction
- limite d'une somme - forme indéterminée
Dans chaque cas, on donne la limite de \(f(x)\) et \(g(x)\).
Déterminer si possible, la limite de \(f(x)+g(x)\) et de \(f(x)-g(x)\) et indiquer les éventuelles
asymptotes.
a) \[\left\{\begin{array}{l}
\lim\limits_{\substack{x \to +\infty}}f(x)=+\infty \\
\lim\limits_{x \to +\infty}g(x)=+\infty \\
\end{array}\right.\]
b) \[\left\{\begin{array}{l}
\lim\limits_{x \to -3}f(x)=+\infty \\
\lim\limits_{x \to -3}g(x)=-\infty \\
\end{array}\right.\]
c) \[\left\{\begin{array}{l}
\lim\limits_{x \to -\infty}f(x)=-\infty \\
\lim\limits_{x \to -\infty}g(x)=-\infty \\
\end{array}\right.\]
d) \[\left\{\begin{array}{l}
\lim\limits_{x \to +\infty}f(x)=-\infty \\
\lim\limits_{x \to +\infty}g(x)=-4 \\
\end{array}\right.\]
Corrigé en vidéo
Exercice 2: Déterminer la
limite d'un
produit, d'un
quotient - forme indéterminée
Dans chaque cas, on donne la limite de \(f(x)\) et \(g(x)\).
Déterminer si possible, la limite de \(f(x)\times g(x)\) et de \(\frac {f(x)}{g(x)}\) et indiquer les éventuelles
asymptotes.
a) \[\left\{\begin{array}{l}
\lim\limits_{x \to 0}f(x)=-\infty \\
\lim\limits_{x \to 0}g(x)=+\infty \\
\end{array}\right.\]
b) \[\left\{\begin{array}{l}
\lim\limits_{x \to -\infty}f(x)=-\infty \\
\lim\limits_{x \to -\infty}g(x)=-3 \\
\end{array}\right.\]
c) \[\left\{\begin{array}{l}
\lim\limits_{x \to +\infty}f(x)=3 \\
\lim\limits_{x \to +\infty}g(x)=-\infty \\
\end{array}\right.\]
d) \[\left\{\begin{array}{l}
\lim\limits_{x \to +\infty}f(x)=0 \\
\lim\limits_{x \to +\infty}g(x)=-\infty \\
\end{array}\right.\]
Corrigé en vidéo
Exercice 3:
limite d'une fonction à l'aide des tableaux - Limite d'un
quotient - forme indéterminée
Dans chaque cas, on donne la limite de \(f(x)\) et \(g(x)\) et le signe de \(g(x)\).
Déterminer si possible, la limite de \(f(x)\times g(x)\) et de \(\frac {f(x)}{g(x)}\) et indiquer les
éventuelles asymptotes.
a) \[\left\{\begin{array}{l}
\lim\limits_{x \to +\infty}f(x)=-\infty \\
\lim\limits_{x \to +\infty}g(x)=0 \\
g(x)>0
\end{array}\right.\]
b) \[\left\{\begin{array}{l}
\lim\limits_{x \to -\infty}f(x)=-4\\
\lim\limits_{x \to -\infty}g(x)=0 \\
g(x)<0
\end{array}\right.\]
c) \[\left\{\begin{array}{l}
\lim\limits_{x \to +\infty}f(x)=0 \\
\lim\limits_{x \to +\infty}g(x)=0 \\
g(x)>0
\end{array}\right.\]
Corrigé en vidéo
Exercice 4: Déterminer la
limite d'une fonction -
forme
indéterminée - Asymptote
Déterminer les limites suivantes et interpréter graphiquement:
a) \[\lim_{x \to -\infty} 2x^3-5x^2+1\]
b) \[\lim_{x \to +\infty}
2x^3-5x^2+1\]
Corrigé en vidéo
Exercice 5: Déterminer la
limite d'une fonction - Lever
l'
indétermination en factorisant par le terme de plus haut degré
Déterminer les limites suivantes. Indiquer les équations des éventuelles asymptotes horizontales ou
verticales:
a) \[\lim_{x \to +\infty} \frac 2 {1-x}\]
b) \[\lim_{x \to -\infty}
\frac{x^3+x-1}{2x^2+x}\]
c) \[\lim_{x \to +\infty} (2x-3)\times
\frac{1}{x+1}\]
Corrigé en vidéo
Exercice 6: Déterminer la
limite d'une fonction -
Limite à
gauche -
Limite à droite
Déterminer les limites suivantes:
a) \[\lim_{\substack{x \to 2\\x<2}} \frac{1-3x}{2-x}\]
b) \[\lim_{\substack{x \to 2\\x>2}}
\frac{1-3x}{2-x}\]
Corrigé en vidéo
Exercice 7: Déterminer la
limite d'une fonction -
Limite à
gauche -
Limite à droite
Déterminer les limites suivantes. Indiquer les équations des éventuelles asymptotes horizontales ou
verticales:
a) \[\lim_{\substack{x \to 0\\x<0}} 4+\frac{1}{x}-\frac{2}{x^2}\]
b) \[\lim_{\substack{x \to 0\\x>0}}
4+\frac{1}{x}-\frac{2}{x^2}\]
c) \[\lim_{\substack{x \to +\infty}}
4+\frac{1}{x}-\frac{2}{x^2}\]
Corrigé en vidéo
Exercice 8: Déterminer la
limite d'une fonction -
Limite à
gauche -
Limite à droite -
forme indéterminée
Déterminer les limites suivantes. Indiquer les équations des éventuelles asymptotes horizontales ou
verticales:
a) \[\lim_{\substack{x \to 1\\x>1}} \frac{2x+5}{1-x}\]
b) \[\lim_{\substack{x \to 1\\x<1}}
\frac{2x+5}{1-x}\]
c) \[\lim_{\substack{x \to -\infty}}
\frac{2x+5}{1-x}\]
Corrigé en vidéo
Exercice 9: Déterminer la
limite d'une fonction -
Limite à
gauche -
Limite à droite
Déterminer les limites suivantes:
a) \[\lim_{\substack{x \to 1\\x<1}} \frac{x+3}{x^2-1}\]
b) \[\lim_{\substack{x \to 1\\x>1}}
\frac{x+3}{x^2-1}\]
Exercice 10: Déterminer la
limite d'une fonction en a - limite à gauche
et à droite
Déterminer les limites suivantes, en distinguant si besoin, la limite à gauche et à droite.
Indiquer les équations des éventuelles asymptotes horizontales ou verticales.
a) \[\lim_{\substack{x \to 2}} \frac1{(x-2)^2}\]
b) \[\lim_{\substack{x \to 2}}
\frac1{x-2}\]
c) \[\lim_{\substack{x \to 1}} \frac
x{x^2-1}\]
d) \[\lim_{\substack{x \to -\infty}} \frac
x{x^2-1}\]
Corrigé en vidéo
Exercice 11:
limite d'une fonction -
limite d'une
composée
Déterminer les limites suivantes:
a) \[\lim_{x \to -\infty} \cos \left(\frac 1x\right)\]
b) \[\lim_{\substack{x \to +\infty}} \sqrt \frac
{4x+5}{x-2}\]
c) \[\lim_{\substack{x \to 2\\x>2}} \sqrt \frac
{4x+5}{x-2}\]
Corrigé en vidéo
Exercice 12:
limite de fonction dans le cas
\(\frac
00\) - Utiliser la dérivation
Déterminer les limites suivantes:
a)
\[\lim_{x \to 1} \frac {\sqrt x -1}{x-1}\]
b)
\[\lim_{x \to 0} \frac {\sin x }{x}\]
c)
\[\lim_{x \to -1} \frac {x^3-5x-4}{x+1}\]
1) Faire apparaitre: \[\frac{f(x)-f(a)}{x-a}\]
en précisant f.
2) Conclure en utilisant la propriété:
Si f est dérivable en a alors \[\lim_{x \to a}
\frac{f(x)-f(a)}{x-a}=f'(a)\]
Exercice 13: Démontrer qu'une
fonction n'a pas de limite -
limite de la fonction cosinus et sinus en +∞
On considère la fonction définie sur \(\mathbb{R}\) par \(f(x)=\cos(x)\).
1) Démontrer qu'on ne peut avoir \[\lim_{\substack{x \to +\infty}} f(x)=+\infty\],
ni \[\lim_{\substack{x \to +\infty}} f(x)=-\infty\].
2) Calculer \(f(2\pi n)\) et \(f(2\pi n+\pi)\) où \(n\) est un entier naturel.
3) En déduire que \(f\) n'a pas de limite finie en \(+\infty\).
4) Que peut-on conclure?
5) Comment adapter cette méthode, pour montrer que la fonction sinus n'a pas de limite.
Exercice 14:
Limite d'une fonction décroissante
On considère une fonction \(f\) définie et décroissante sur \(\mathbb{R}\). On sait de plus \[\lim_{\substack{x \to +\infty}} f(x)=1\].
1) Quelle conjecture peut-on faire sur \(f\)?
2) Démontrer cette conjecture.
Corrigé en vidéo
Exercice 15:
Limite d'une fonction à l'aide d'un encadrement - sinus -
cosinus - Théorème des gendarmes
Déterminer les limites suivantes:
a) \[\lim_{\substack{x \to +\infty}} x+\cos(x)\]
b) \[\lim_{\substack{x \to +\infty}}
\frac{3x-1}{x-2\sin(x)}\]
c) \[\lim_{\substack{x \to -\infty}}
\frac{\sin(x)}{x+\cos(x)}\]
Corrigé en vidéo
Exercice 16:
Limite d'une fonction à l'aide d'un encadrement - sinus -
cosinus - Théorème des gendarmes
Déterminer les limites suivantes:
\[\lim_{\substack{x \to +\infty}} \frac{\sin 2x}{x}\]
\[\lim_{\substack{x \to 0}} \frac{\sin
2x}{x}\]
\[\lim_{\substack{x \to 0}}
\frac{x+\sin(x)}{x}\]
\[\lim_{\substack{x \to +\infty}}
\frac{x+\sin(x)}{x}\]
Corrigé en vidéo
Exercice 17:
Théorème de comparaison et des gendarmes pour trouver la limite
d'une fonction
Dans chaque cas, on considère une fonction $f$ définie sur $]0;+\infty[$ vérifiant une condition donnée.
Déterminer, si possible, la limite de $f$ en $+\infty$ et en 0:
1) Pour tout $x>0$, \[~f(x)\ge \frac 1x\].
2) Pour tout $x\ge 1$, \[~\frac{x-1}{x+1}\le f(x)\le \frac 1x
+1\].
3) Pour tout $x>0$, \[~|6-2f(x)|\le \frac 1x\].
Exercice 18:
Limite d'une fonction à l'aide d'un encadrement - ...≤
f(x) ≤ ... - théorème des gendarmes
1) \(f\) est une fonction définie sur \(]0;+\infty[\) telle que \(f(x)\le \frac 1x\)
a) Déterminer si possible \[\lim_{\substack{x \to
+\infty}}f(x)\] . Justifier votre réponse.
b) Déterminer si possible \[\lim_{\substack{x \to 0}}f(x)\]
. Justifier votre réponse.
2) \(f\) est une fonction définie sur \(]0;+\infty[\) telle que \(f(x)\ge \frac 1x\)
a) Déterminer si possible \[\lim_{\substack{x \to
+\infty}}f(x)\] . Justifier votre réponse.
b) Déterminer si possible \[\lim_{\substack{x \to 0}}f(x)\]
. Justifier votre réponse.
3) \(f\) est une fonction définie sur \(]0;+\infty[\) telle que pour \(x\ge 1\), \(\frac 1{x^2} \le f(x)\le
\frac 1x\)
a) Déterminer si possible \[\lim_{\substack{x \to
+\infty}}f(x)\] . Justifier votre réponse.
b) Déterminer si possible \[\lim_{\substack{x \to 0}}f(x)\]
. Justifier votre réponse.
4) \(f\) est une fonction définie sur \(]0;+\infty[\) telle que pour \(x\ge 1\), \(1-\frac 1{x} \le 2f(x)-5\le
1+\frac 1{x^2}\)
Déterminer si possible \[\lim_{\substack{x \to
+\infty}}f(x)\] . Justifier votre réponse.
5) \(f\) est une fonction définie sur \([0;+\infty[\) telle que pour \(x\ge 0\), \(0 \le f(x)\le
\sqrt{x}\)
a) Déterminer si possible \[\lim_{\substack{x \to
+\infty}}f(x)\] . Justifier votre réponse.
b) Déterminer si possible \[\lim_{\substack{x \to 0}}f(x)\]
. Justifier votre réponse.
c) Déterminer si possible \[\lim_{\substack{x \to
+\infty}}\frac{f(x)}{x}\] . Justifier votre réponse.
Exercice 19:
Limite d'une fonction à l'aide d'un encadrement -
|
f(x)-l| ≤ ...
On considère une fonction \(f\) définie sur \(]0;+\infty[\) par \(f(x)=\frac{x^2+x-1}{2x^2}\).
1) A l'aide d'une calculatrice, conjecturer la limite \(\ell\) de \(f\) en \(+\infty\).
2) Démontrer que pour \(x\ge 1\), \(|f(x)-\ell|\le \frac 1 {2x}\).
3) En déduire \[\lim_{\substack{x \to +\infty}}f(x)\] .
4) Retrouver la limite de \(f\) en \(+\infty\) sans utiliser d'encadrement.
Exercice 20:
Lecture limite graphiquement - limite d'une somme, d'un
produit, d'un quotient, d'une composée - asymptote
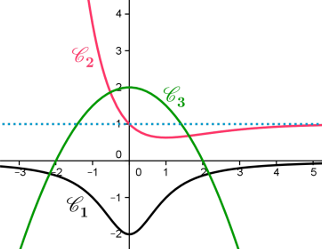
\(\mathscr{C}_1\), \(\mathscr{C}_2\),\(\mathscr{C}_3\) sont les courbes respectives de 3 fonctions \(f\), \(g\)
et \(h\) définies sur \(\mathbb{R}\).
| 1) |
Déterminer graphiquement les limites de \(f\), \(g\) et \(h\) en \(+\infty\) et \(-\infty\).
|
|
Indiquer les asymptotes horizontales ou verticales. |
| 2) |
Déterminer si possible, les limites suivantes: |
|
a) \[\lim_{\substack{x \to +\infty}} f(x)+g(x)\] |
b) \[\lim_{\substack{x \to -\infty}} g(x)\times h(x) \] |
c) \[\lim_{\substack{x \to -\infty}} f(x)\times h(x)\] |
d) \[\lim_{\substack{x \to +\infty}} f(x)\times g(x) \] |
|
e) \[\lim_{\substack{x \to -\infty}} g(x)+ h(x) \] |
f) \[\lim_{\substack{x \to -\infty}} h(x)-g(x) \] |
g) \[\lim_{\substack{x \to +\infty}} \frac {h(x)}{g(x)} \] |
h) \[\lim_{\substack{x \to +\infty}} \frac {g(x)}{f(x)} \] |
|
i) \[\lim_{\substack{x \to -\infty}} \frac {h(x)}{g(x)} \] |
j) \[\lim_{\substack{x \to -\infty}} \frac {g(x)}{f(x)} \] |
k) \[\lim_{\substack{x \to -\infty}} f(-x) \] |
l) \[\lim_{\substack{x \to -\infty}} f(g(x)) \] |
Corrigé en vidéo
Exercice 21:
Limite et tableau de variation -
asymptote - limite de -f , 1/f et de |f|
On donne le tableau de variations d'une fonction \(f\) définie sur \(\mathbb{R}\backslash\{ -3 \}\).
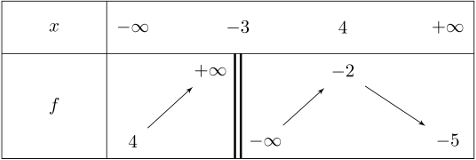
- Déterminer les limites de \(f\) aux bornes du domaine de définition.
Indiquer les équations des éventuelles asymptotes.
- Déterminer le tableau de variations des fonctions \(-f\), \(\frac 1f\) et \(|f|\).
Préciser dans chaque cas, les limites aux bornes du domaine de définition.
Corrigé en vidéo
Exercice 22:
Déterminer a,b,c - à l'aide du
tableau de
variation et des limites
On connait le tableau de variations d'une fonction \(f\):
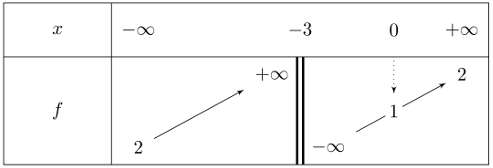
On sait de plus qu'il existe trois réels \(a\), \(b\), \(c\) tels que pour tout \(x\ne-3\),
\(f(x)=\frac{ax+b}{x+c}\).
Déterminer les valeurs de \(a\), \(b\), \(c\) en justifiant.
Corrigé en vidéo
Exercice 23: Déterminer
a,b,c tels que f(x)=ax+b+... - Etude complète
d'une fonction - variation - limite - asymptote
On considère la fonction \(f\) définie sur \(\mathbb{R}\backslash\{ 2 \}\) par \(\displaystyle
f(x)=\frac{2x^2-3x-3}{x-2}\).
- Déterminer la limite de \(f\) en \(+\infty\) et \(-\infty\).
- Déterminer \[\lim_{\substack{x \to 2\\x>2}}f(x)\] et \[\lim_{\substack{x \to 2\\x<2}}f(x)\]
- Déterminer \(f'(x)\).
- Dresser le tableau de variation de \(f\)
Préciser dans ce tableau les limites aux bornes du domaine de définition.
Indiquer les équations des éventuelles asymptotes.
- Déterminer les réels \(a\), \(b\) et \(c\) tels que pour tout \(x\ne 2\), \(\displaystyle f(x)=ax+b+\frac
{c}{x-2}\).
- Déterminer \[\lim_{\substack{x \to +\infty}}f(x)-(ax+b)\]
Quelle interprétation graphique peut-on en déduire?
Vérifier cette interprétation à l'aide de la calculatrice.
Corrigé en vidéo
Exercice 24:
Limite et racine -
quantité conjuguée
On considère la fonction \(f\) définie sur \(\mathbb{R}\) par \(f(x)=x-\sqrt{x^2+5}\).
1) Déterminer la limite de \(f\) en \(-\infty\).
2) Déterminer la limite de \(f\) en \(+\infty\). On pourra utiliser l'expression conjuguée
.
L'expression conjuguée de:
\[a-\sqrt b\] est \[a+\sqrt
b\]
1) Multiplier et diviser par l'expression conjuguée
2) Développer, arranger
3) Chercher la limite
Exercice 25: Déterminer une fonction connaissant les limites
Dans chaque cas, déterminer une fonction \(f\) vérifiant les conditions suivantes:
a) \[\lim_{\substack{x \to 1\\x<1}}f(x)=-\infty\] et \[\lim_{\substack{x \to 1\\x>1}}f(x)=+\infty\] et \[\lim_{\substack{x \to +\infty}}f(x)=0\]
b) \[\lim_{\substack{x \to 1\\x<1}}f(x)=-\infty\] et \[\lim_{\substack{x \to 1\\x>1}}f(x)=-\infty\] et \[\lim_{\substack{x \to +\infty}}f(x)=2\]
c) \[\lim_{\substack{x \to -\infty}}f(x)=3\] et \[\lim_{\substack{x \to +\infty}}f(x)=2\]
Web
