Intégrale - exercices type BAC

$n$ désigne un entier naturel non nul. On pose $\displaystyle u_n=\int_{0}^1 x^ne^{-x}\: \text{d}x$.
$f_n$ désigne la fonction définie sur [0;1] par $f_n(x)=x^ne^{-x}$. $\mathscr{C}_n$ désigne la courbe représentative de $f_n$.
1) A l'aide du graphique, conjecturer:
    a) le sens de variations de la suite $(u_n)$.
    b) la limite de la suite $(u_n)$.
2) Démontrer la conjecture du 1.a).
3) Démontrer que la suite $(u_n)$ est convergente.
4) Démontrer que pour tout entier naturel $n$ non nul:
    $\displaystyle ~~~~ ~~~~~ 0\leqslant u_n\leqslant \frac 1{n+1}$.
5) Que peut-on en déduire?

Soit $f$ et $h$ les fonctions définies sur $\mathbb{R}$ par $f(x) = \dfrac{3}{1 + \text{e}^{- 2x}}$ et $h(x)=3-f(x)$.
1. Justifier que la fonction $h$ est positive sur $\mathbb{R}$.
2. Soit $H$ la fonction définie sur $\mathbb{R}$ par $H(x) = - \dfrac{3}{2} \ln \left(1 + \text{e}^{- 2x}\right)$.
     Démontrer que $H$ est une primitive de $h$ sur $\mathbb{R}$.
3. Soit $a$ un réel strictement positif.
     a. Donner une interprétation graphique de l'intégrale $\displaystyle\int_0^a h(x)\:\text{d}x$.
     b. Démontrer que $\displaystyle\int_0^a h(x)\:\text{d}x = \dfrac{3}{2} \ln \left(\dfrac{2}{1 + \text{e}^{- 2a}}\right)$.
     c. On note $\mathcal{D}$ l'ensemble des points $M(x~;~y)$ du plan définis par $\left\{\begin{array}{l c l} x\geqslant 0\\ f(x) \leqslant y\leqslant 3 \end{array}\right.$.
         Déterminer l'aire, en unité d'aire, du domaine $\mathcal{D}$.

On considère la fonction \(f\) définie sur \([0;+\infty[\) par \[f(x)=5 e^{-x} - 3e^{-2x} + x - 3\].
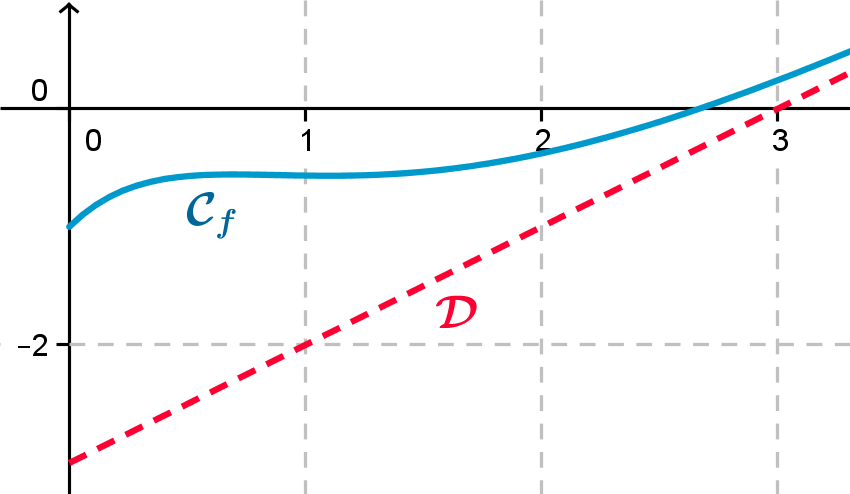
On note \(\mathcal{C}_{f}\) la représentation graphique de la fonction \(f\) et \(\mathcal{D}\) la droite d'équation \(y = x - 3\)
dans un repère orthogonal du plan. On considère la fonction \(\mathcal{A}\)
définie sur \([0;+\infty[\) par \[\mathcal{A}(x) = \displaystyle\int_{0}^x f(t) - (t - 3)\: \text{d}t.\]
1. Justifier que, pour tout réel \(t\) de \([0;+\infty[\), \(\:f(t)-(t-3)> 0\).
2. Hachurer sur le graphique ci-contre, le domaine
    dont l'aire est donnée par \(\mathcal{A}(2)\).
3. Justifier que la fonction \(\mathcal{A}\) est croissante sur \([0;+\infty[\).
4. Pour tout réel \(x\ge 0\), calculer \(\mathcal{A}(x)\).
5. Existe-t-il une valeur de \(x\) telle que \(\mathcal{A}(x) = 2\) ?

L'objectif de cet exercice est de calculer: \[\displaystyle\int_{-1}^1 \sqrt{1-x^2}\: \text{d}x.\]
On considère la fonction $f$ définie par $f(x)=\sqrt{1-x^2}$.
1) Déterminer le domaine de définition de la fonction $f$.
2) Quelle conjecture peut-on faire concernant la courbe de la fonction $f$? Démontrer cette conjecture.
3) En déduire la valeur de l'intégrale \[\displaystyle\int_{-1}^1 \sqrt{1-x^2}\: \text{d}x.\]

Soit un entier $n\geqslant 1$.
On note $f_n$ la fonction définie pour tout réel $x$ de l'intervalle $[0;1]$ par $f_n(x)=\displaystyle\frac 1{1+x^n}$.
Pour tout entier $n\geqslant 1$, on note ${\rm I}_n=\int_{0}^{1} f_n(x) \, \mathrm{d}x$.
1) Déterminer $\rm I_1$.
2) Démontrer que, pour tout réel $x\in [0; 1]$ et pour tout entier $n \geqslant 1$, on a: $\displaystyle 1-x^n\leqslant \frac 1{1+x^n}\leqslant 1$
3) En déduire que la suite $({\rm I}_n)$ est convergente et préciser sa limite.

Pour tout entier $n > 0$, les fonctions $f_n$ sont définies sur l'intervalle $[1~;~5]$ par $f_n(x) = \dfrac{\ln x}{x^n}$.
On note $\mathcal{C}_n$ la courbe représentative de la fonction $f_n$ (ci-dessous $\mathcal{C}_1$, $\mathcal{C}_2$, $\mathcal{C}_3$ et $\mathcal{C}_4$).

1. Montrer que, pour tout entier $n > 0$ et tout réel $x$ de $[1~;~5]$, $f'_n(x) = \dfrac{1- n\ln (x)}{x^{n+1}}$.
2. Pour tout entier $n > 0$, montrer que la fonction $f_n$ admet un maximum sur l'intervalle $[1~;~5]$. On note $A_n$ le point de la courbe $\mathcal{C}_n$ ayant pour ordonnée ce maximum. Montrer que tous les points $A_n$ appartiennent à une même courbe $\Gamma$ d'équation $y = \dfrac{1}{\mathrm{e}} \ln (x)$.
3. 1. Montrer que, pour tout entier $n > 0$ et tout réel $x$ de $[1~;~5]$, $0 \leqslant \dfrac{\ln (x)}{x^n} \leqslant \dfrac{\ln (5)}{x^n}$.
   2. Pour tout entier $n > 0$, on s'intéresse à l'aire, exprimée en unités d'aire, du domaine du plan délimité par les droites d'équations $x = 1$, $x = 5$, $y = 0$ et la courbe $\mathcal{C}_n$. Déterminer la valeur limite de cette aire quand $n$ tend vers $+ \infty$.