



2 droites de l'espace sont soit
|
coplanaires

|
parallèles

|
 strictement parallèle |
Aucun point d'intersection |
 confondues |
Une infinité de points d'intersection | |||
| non parallèles | 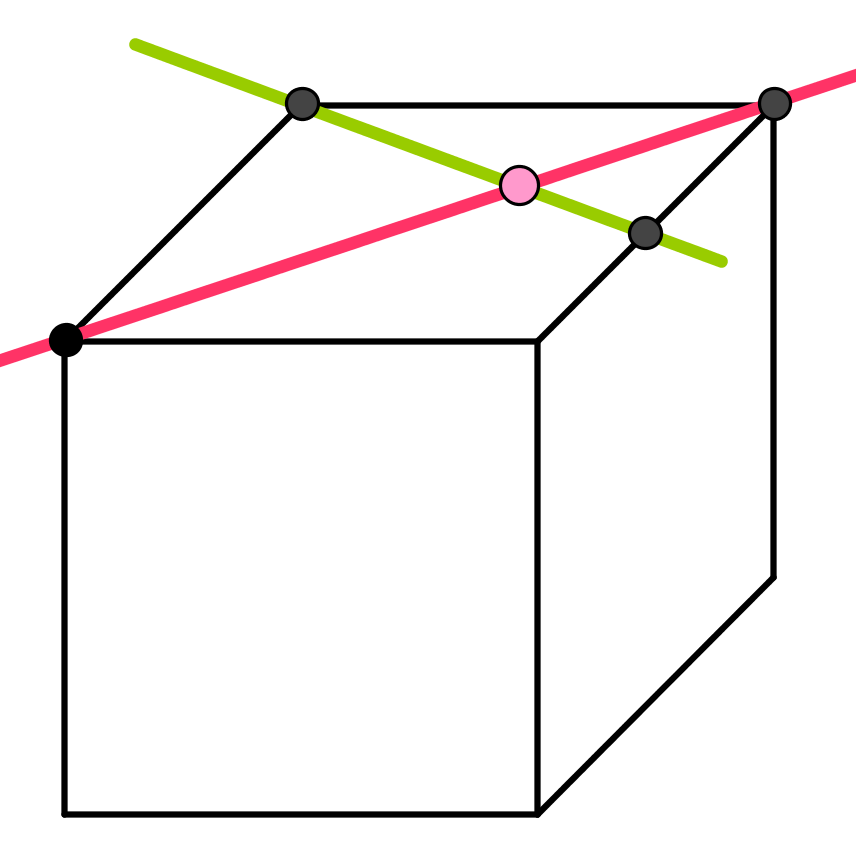 sécantes en 1 point |
1 seul point d'intersection | ||
non coplanaires |
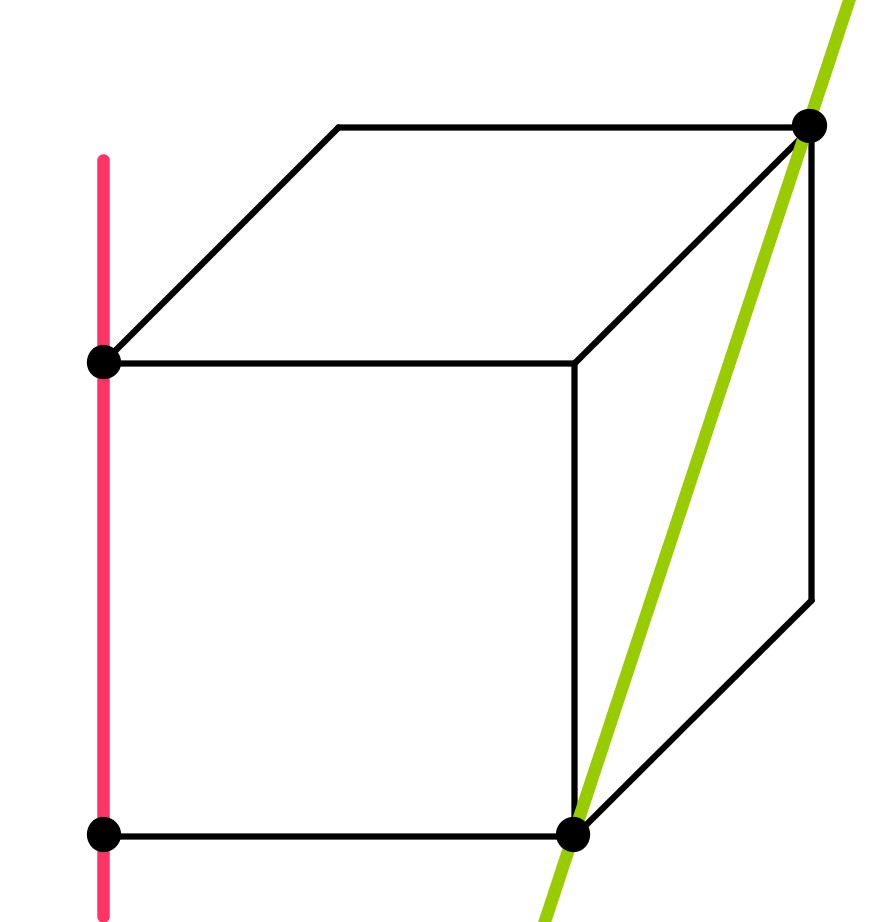 Ni parallèles, ni sécantes |
Aucun point d'intersection |
1 droite et un plan sont soit

|
parallèles

|
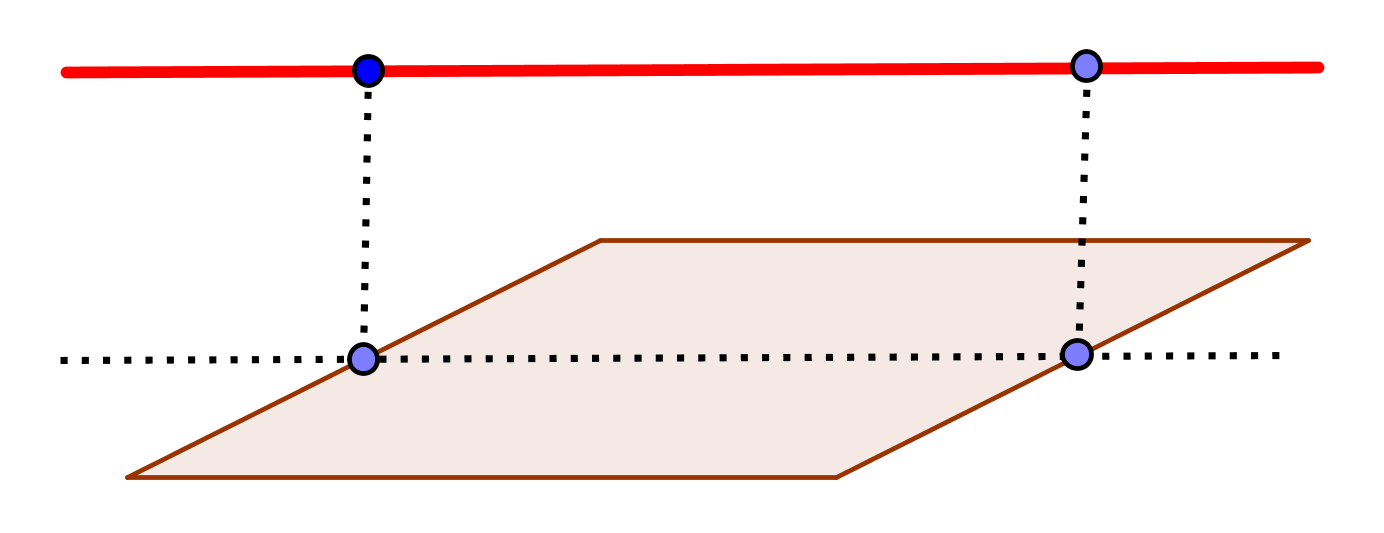 strictement parallèles |
aucun point d'intersection |
 la droite est incluse dans le plan |
une infinité de points d'intersection | ||
| non parallèles | 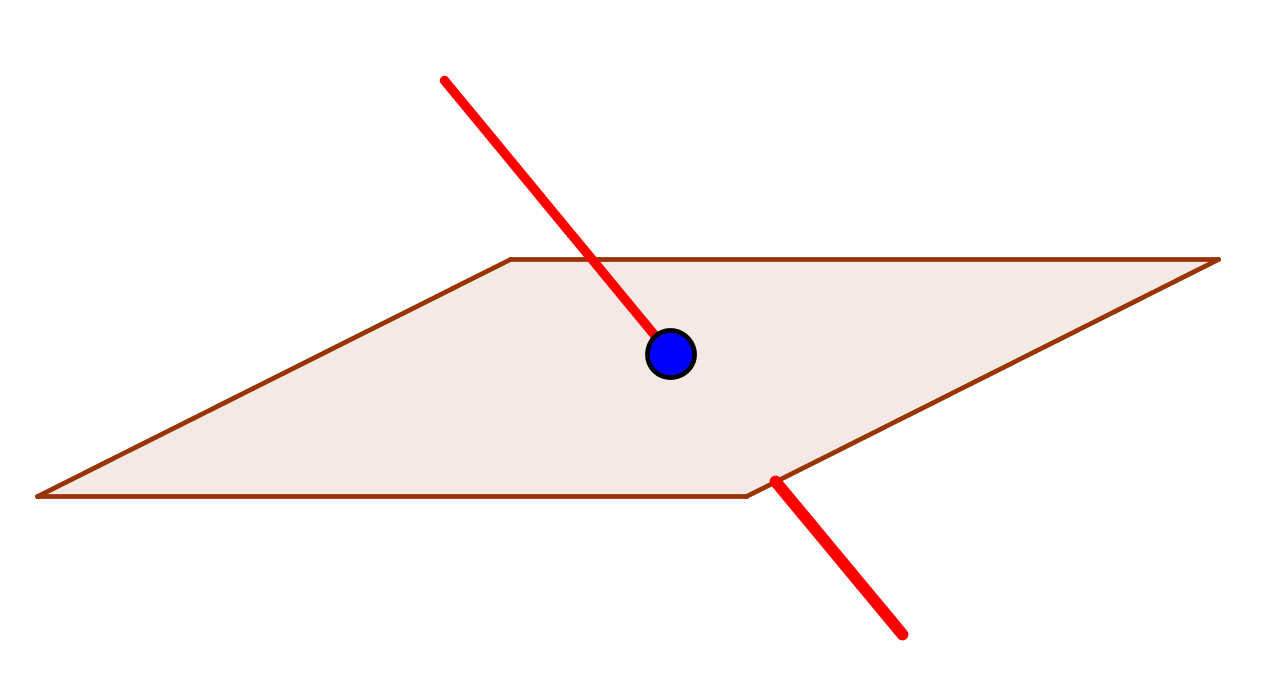 sécants en 1 point |
1 seul point d'intersection |
Deux plans sont soit

|
parallèles

|
 strictement parallèles |
aucun point d'intersection |
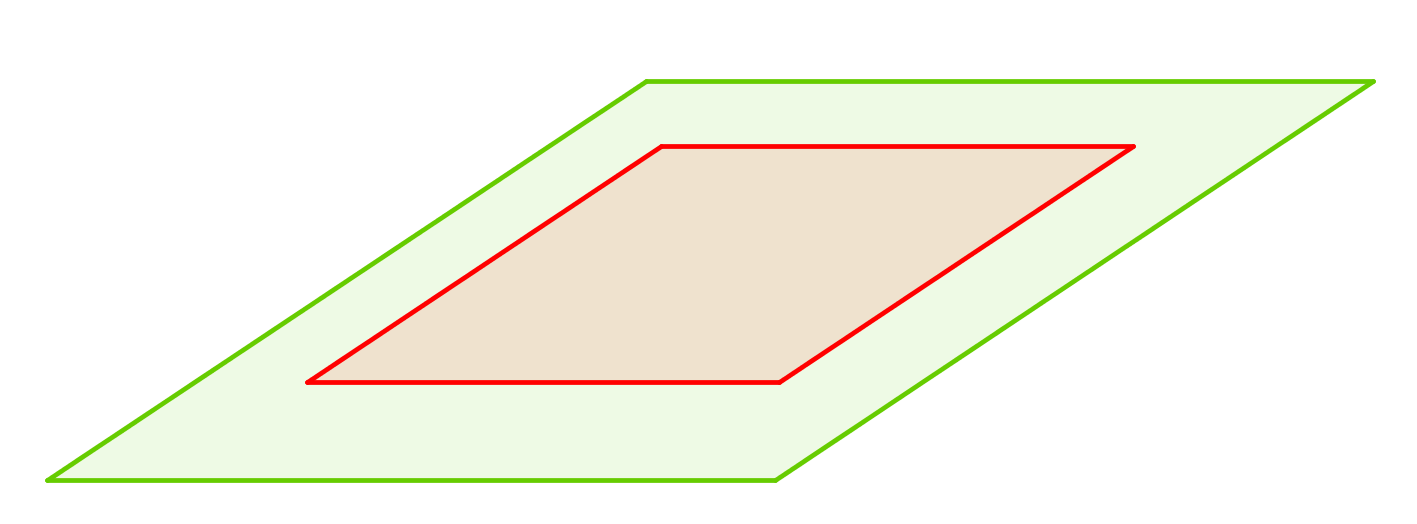 confondus |
une infinité de points d'intersection | ||
| non parallèles | 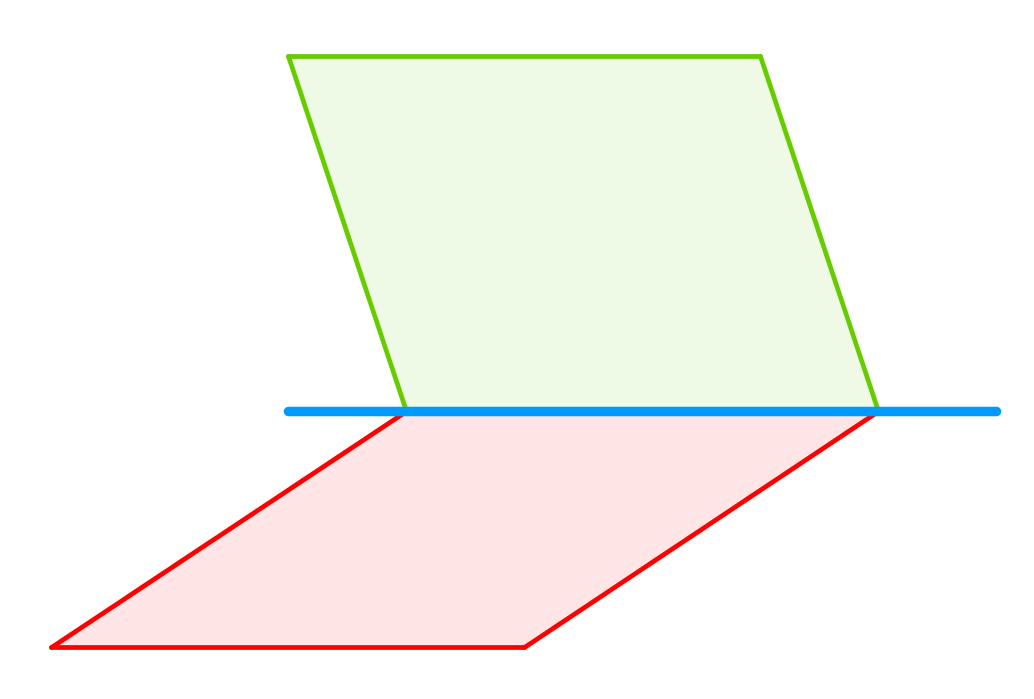 sécants selon une droite |
une infinité de points d'intersection | |





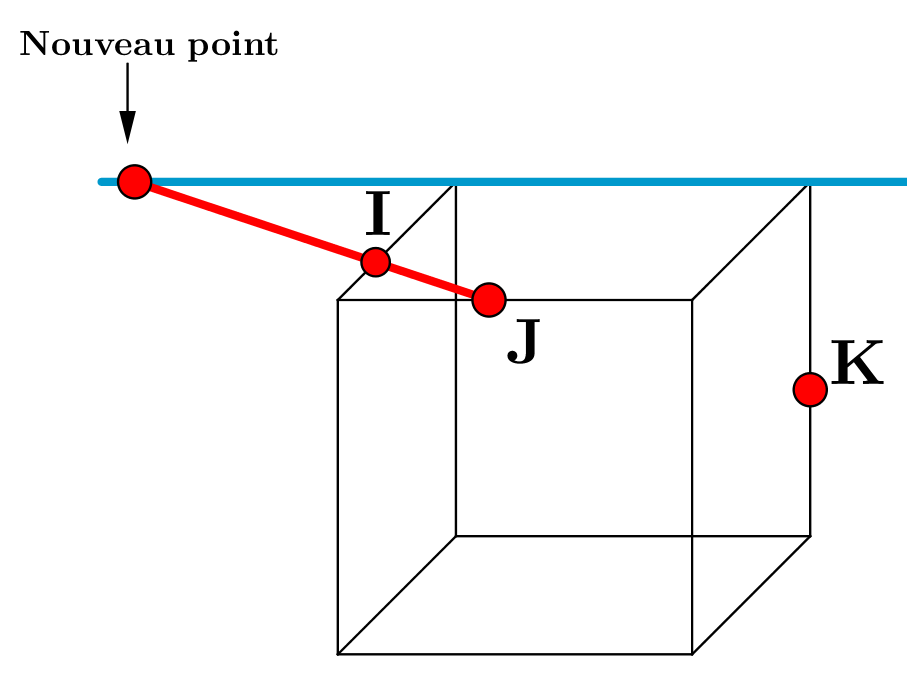

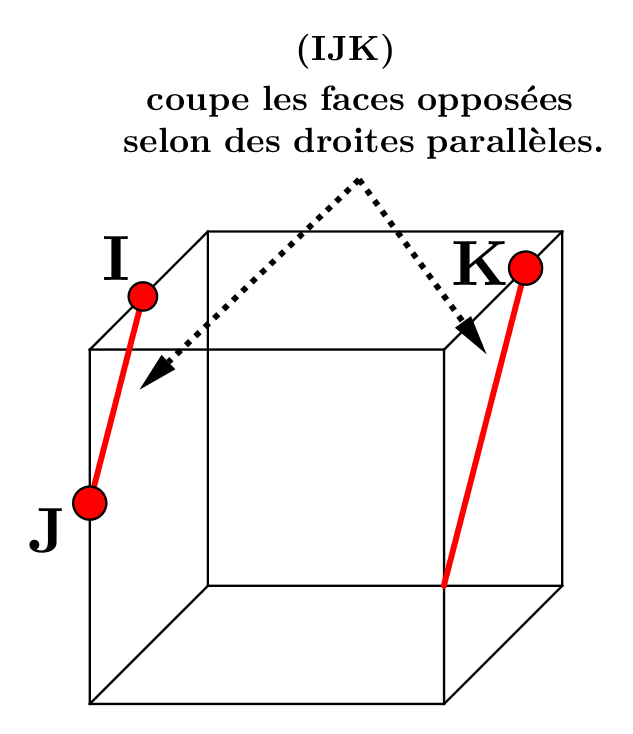
|
|
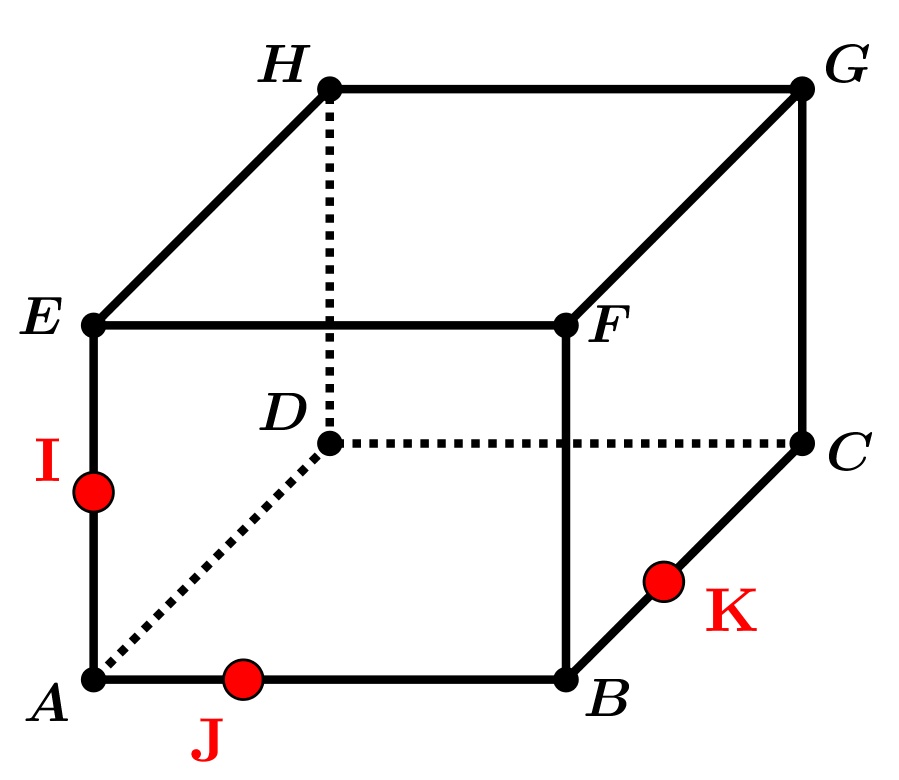



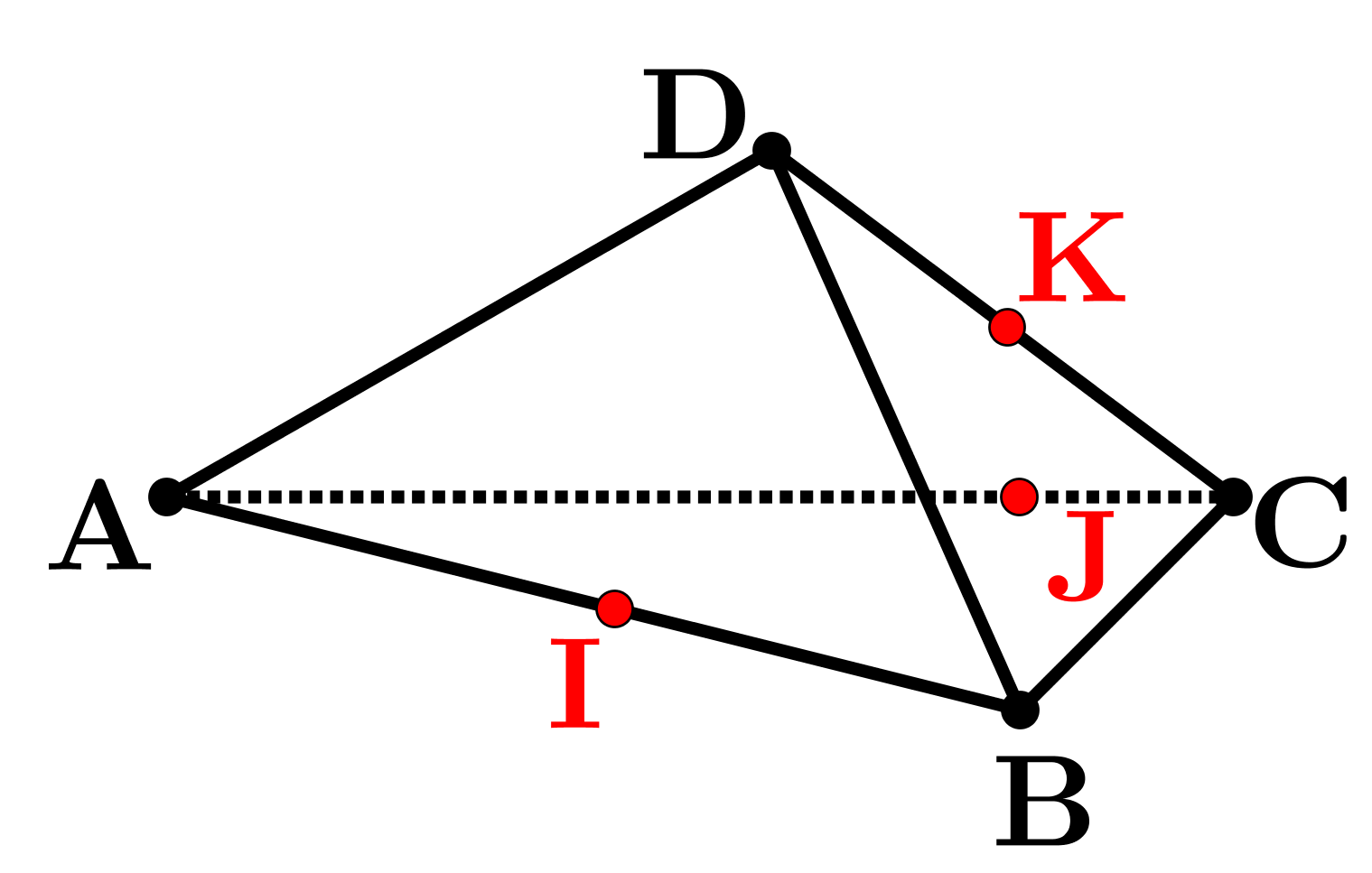



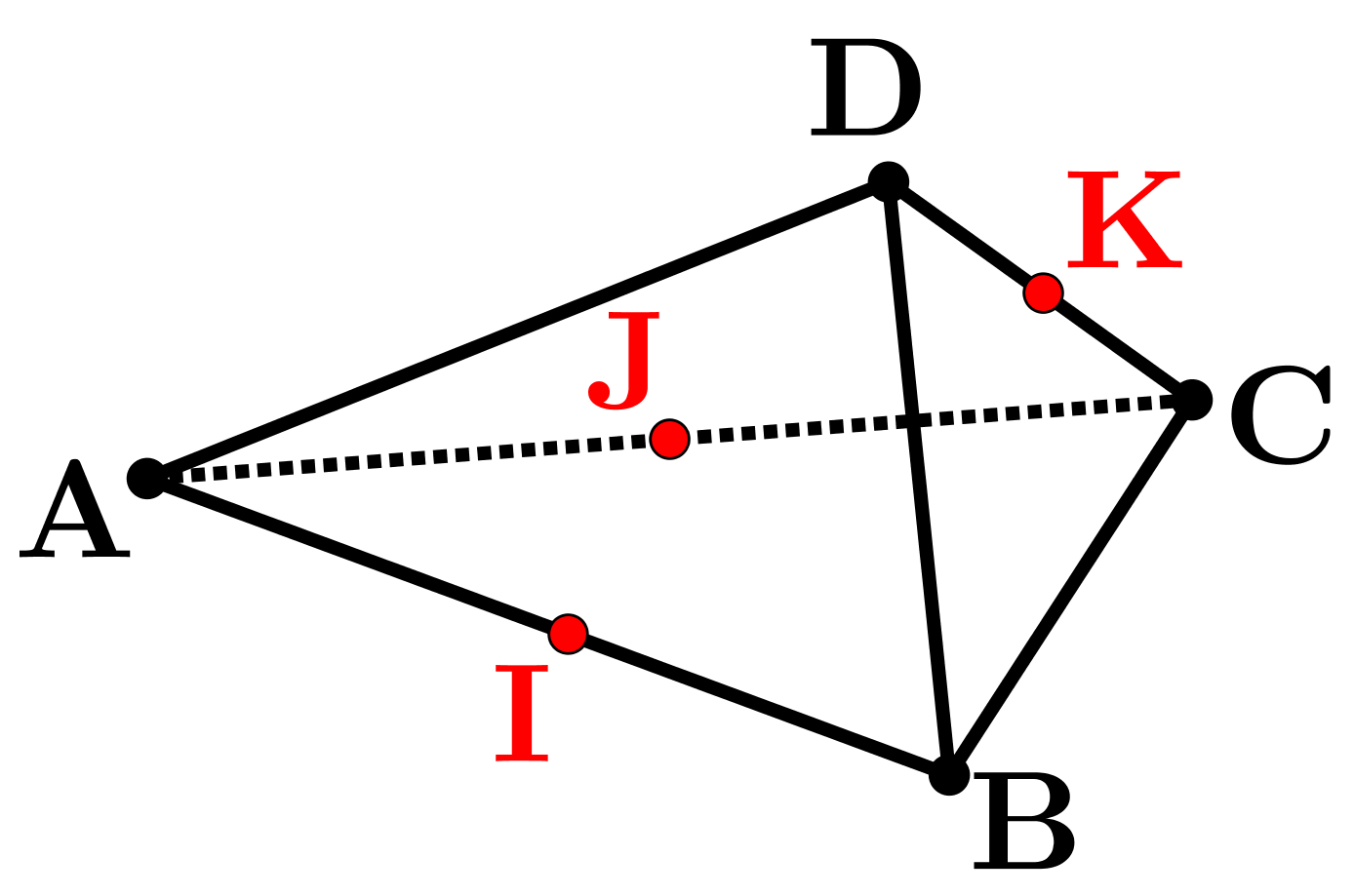










N'hesitez pas à envoyer un mail à:
jaicompris.com@gmail.com