


 Un peu de patience, la vidéo est bientôt prête
Un peu de patience, la vidéo est bientôt prête

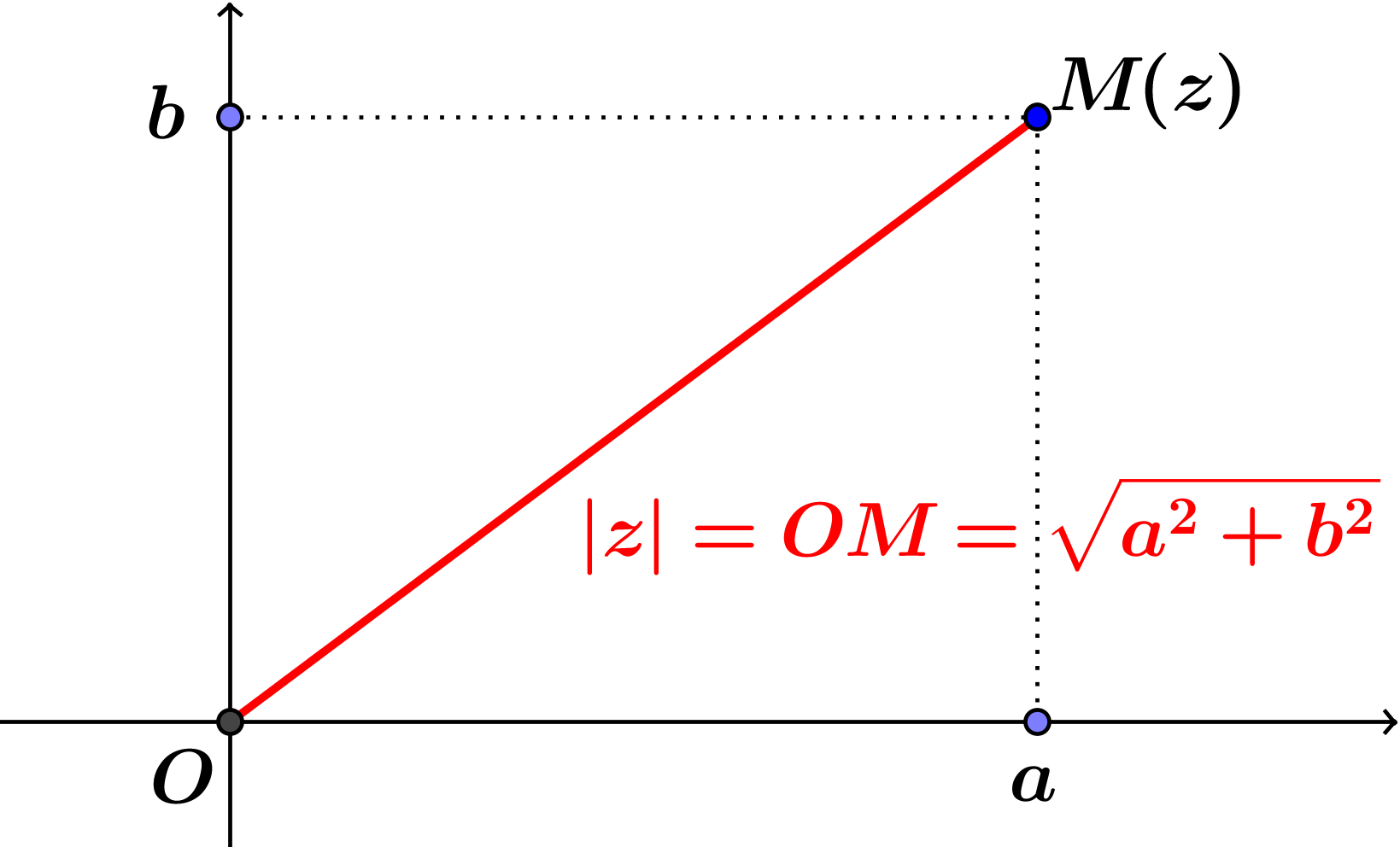
 Un peu de patience, la vidéo est bientôt prête
Un peu de patience, la vidéo est bientôt prête
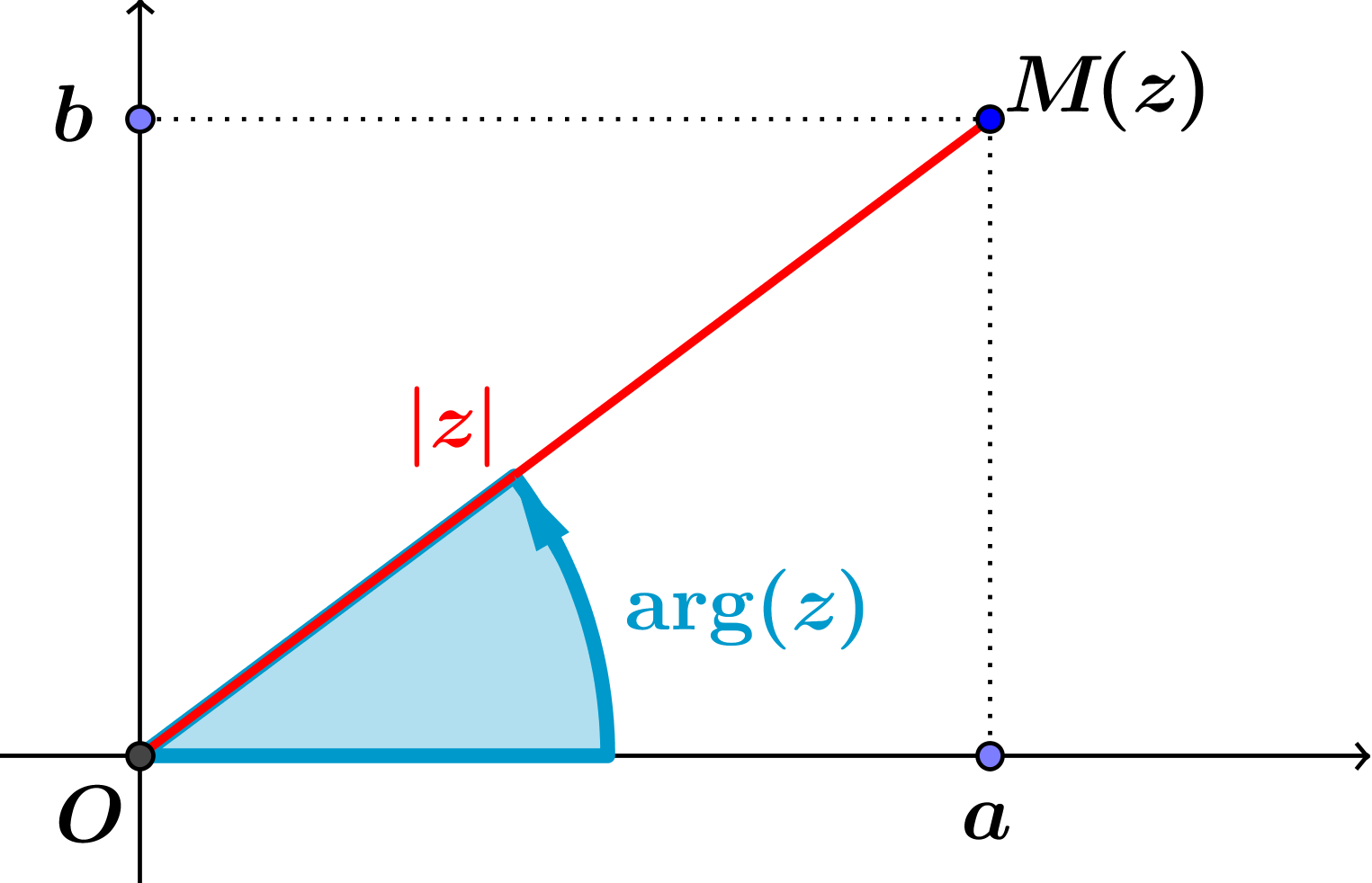

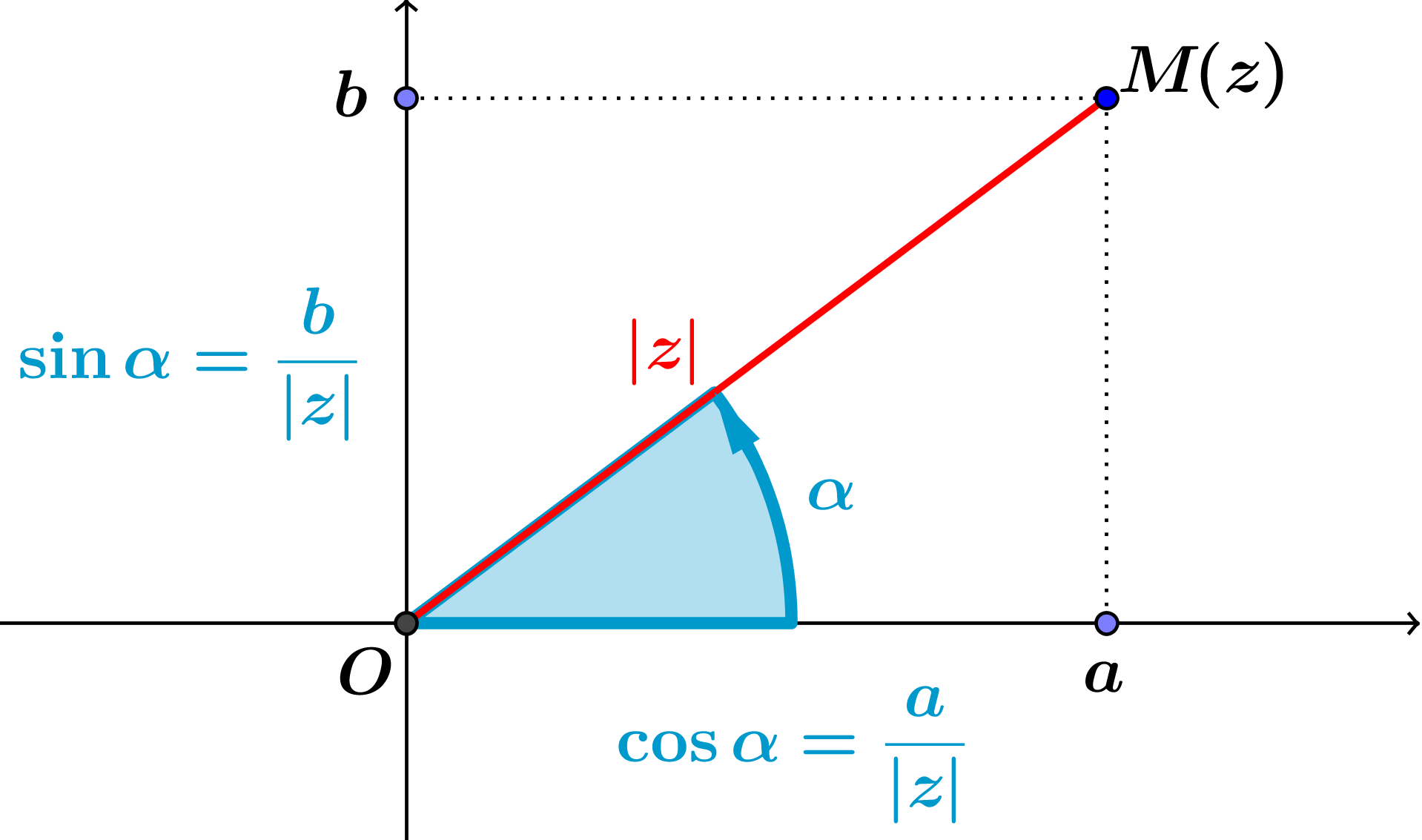
 Un peu de patience, la vidéo est bientôt prête
Un peu de patience, la vidéo est bientôt prête


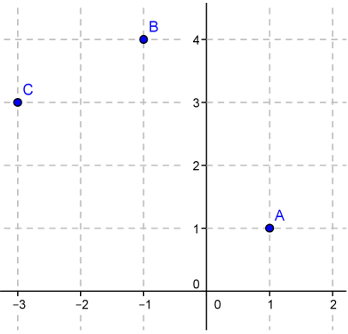










































































N'hesitez pas à envoyer un mail à:
jaicompris.com@gmail.com