


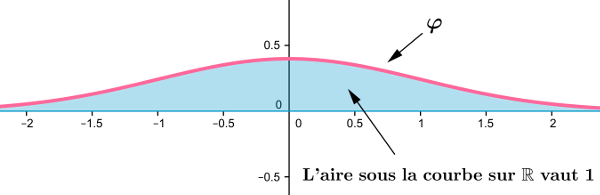
 On note $\varphi$ la fonction définie sur $\mathbb{R}$ par \[\varphi(x)=\frac 1{\sqrt{2\pi}}e^{\frac{-x^2}2}\].
On note $\varphi$ la fonction définie sur $\mathbb{R}$ par \[\varphi(x)=\frac 1{\sqrt{2\pi}}e^{\frac{-x^2}2}\].















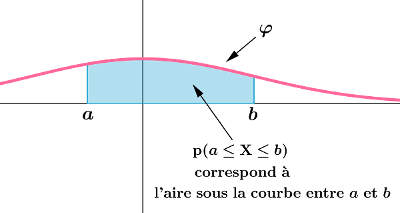
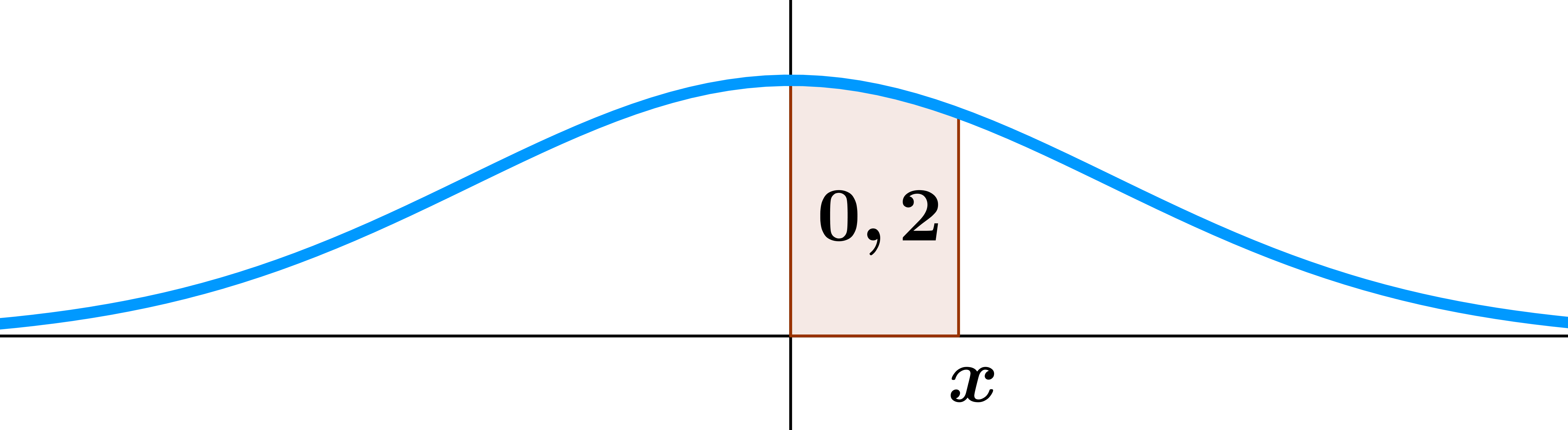
${\rm P}(a\le {\rm X}\le b)=$

\[{\rm P}(a\le {\rm X}\le b)=\int_a^b \varphi(t)~{\rm d}t={\rm P}({\rm X}\le b)-{\rm P}({\rm X}\le a)\]
où $a$ et $b$ sont deux réels tels que $a\le b$ 
Le calcul de l'intégrale se fait à la calculatrice. |
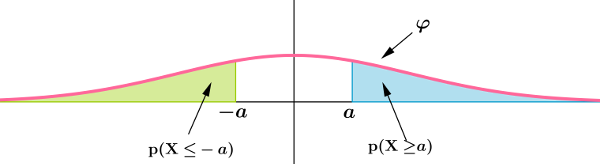
${\rm P(X\ge}a)=$

Par symétrie de la courbe:
\[{\rm P(X\ge}a)={\rm P(X\le}-a)\] où $a$ un réel quelconque. 
Le calcul de l'intégrale se fait à la calculatrice. |
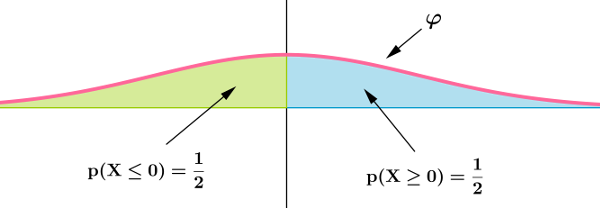
${\rm P}({\rm X} \ge 0)=$

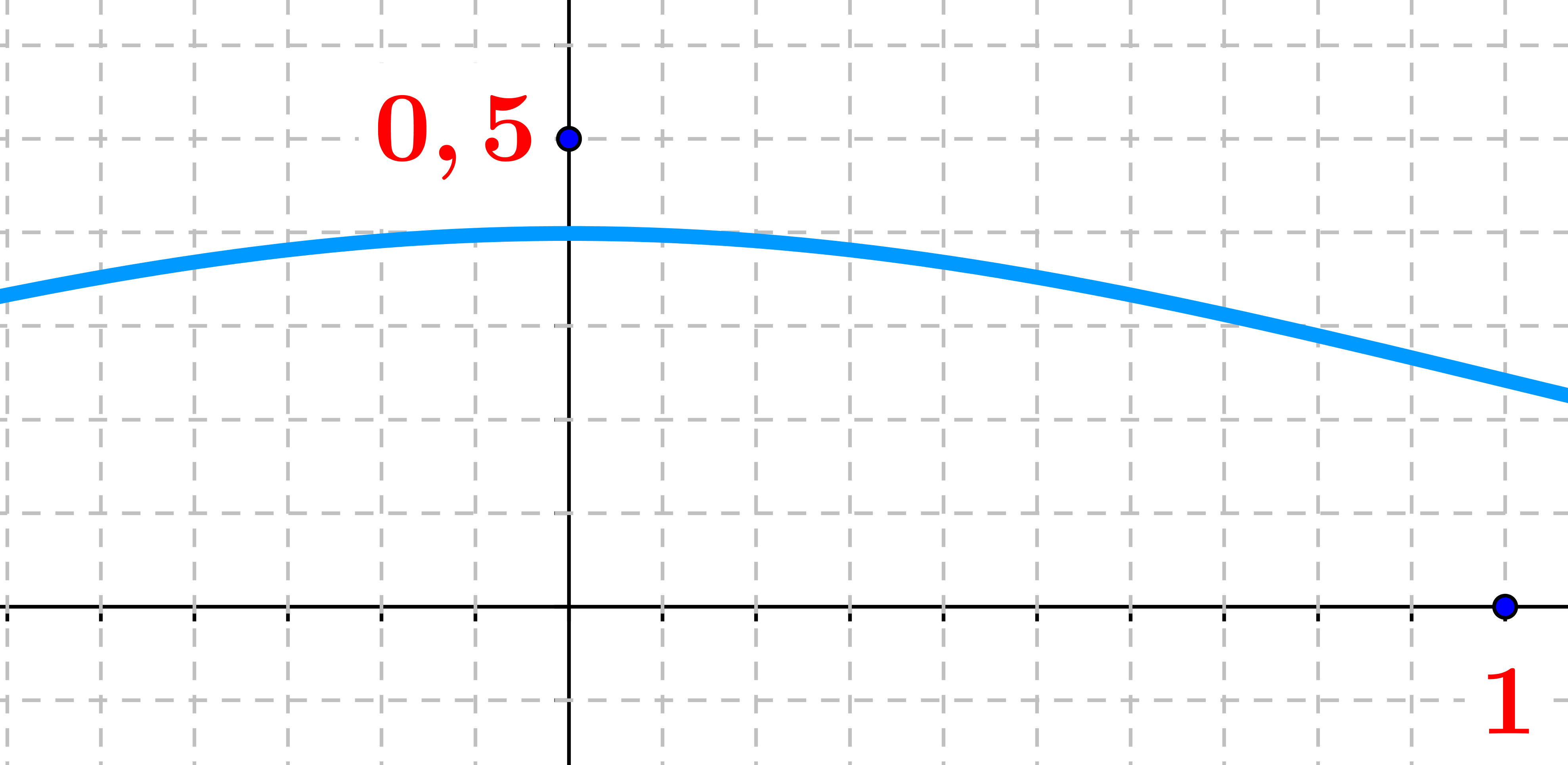
\[{\rm P}({\rm X} \ge 0)=\frac 12\]

|
${\rm P}({\rm X}\le 0)=$

\[{\rm P}({\rm X}\le 0)=\frac 12\]


|






 ♦
Comment calculer $u_{\alpha}$
♦
Comment calculer $u_{\alpha}$

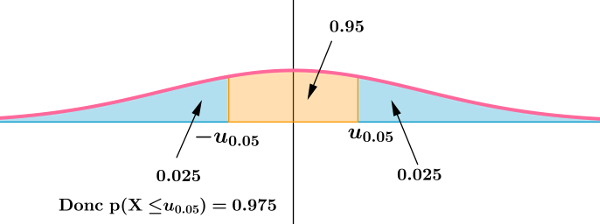








|
|





































N'hesitez pas à envoyer un mail à:
jaicompris.com@gmail.com