Matrice suite et évolution - graphe probabiliste

Matrice et évolution

♦ Matrice et évolution - Graphe - ${\rm X}_{n+1}={\rm A}{\rm X}_n$ et ${\rm X}_{n+1}={\rm A}{\rm X}_n+{\rm B}$ - cours en vidéo

Arbre pondéré et suite

Il est très important de savoir
traduire une situation qui évolue à l'aide d'un arbre pondéré

Exemple:
Si Rose est à l'heure un jour, elle sera à l'heure le lendemain avec une probabilité de $0,3$
Si Rose est en retard un jour, elle sera à l'heure le lendemain avec une probabilité de $0,8$.

${\rm A}_n$ est l'événement: " Rose est à l'heure le n-ième jour."

${\rm B}_n$ est l'événement: " Rose est en retard le n-ième jour."

$\boldsymbol{0,3}$

$\boldsymbol{0,3}$ est la probabilité que Rose arrive à l'heure le jour $n+1$ sachant
qu'elle est arrivée à l'heure le jour $n$.

$\boldsymbol{0,7}$

Pour trouver $\boldsymbol{0,7}$, on utilise le fait que
la somme des probabilités qui partent d'un même noeud est égale à 1.
$\boldsymbol{0,3+0,7=1}$

$\boldsymbol{0,2}$

Pour trouver $\boldsymbol{0,2}$, on utilise le fait que
la somme des probabilités qui partent d'un même noeud est égale à 1.
$\boldsymbol{0,8+0,2=1}$

$\boldsymbol{a_n}$

$\boldsymbol{a_n}$ est la probabilité que Rose arrive à l'heure le n-ième jour.

$\boldsymbol{b_n}$

$\boldsymbol{b_n}$ est la probabilité que Rose arrive en retard le n-ième jour.

$\boldsymbol{0,8}$

$\boldsymbol{0,8}$ est la probabilité que Rose arrive à l'heure le jour $n+1$ sachant
qu'elle est en retard le jour $n$.

On en déduit:
$\left \{ \begin{array}{l } {\rm P}({\rm A}_{n+1})=a_{n+1}=0,3a_n+0,8b_n \\ {\rm P}({\rm B}_{n+1})=b_{n+1}=0,7a_n+0,2b_n \\ \end{array} \right.$

D'après la formule des probabilités totales
Graphe probabiliste et suite

Il est très important de savoir
traduire une situation qui évolue à l'aide d'un graphe probabiliste

Exemple:
Si Rose est à l'heure un jour, elle sera à l'heure le lendemain avec une probabilité de $0,3$
Si Rose est en retard un jour, elle sera à l'heure le lendemain avec une probabilité de $0,8$.

Graphe probabiliste correspondant à la situation:

$\boldsymbol{0,3}$ est la probabilité de rester à l'heure,
c'est à dire que Rose soit à l'heure un jour
sachant que le jour précedent elle était à l'heure.

A est l'état qui correspond au fait d'être à l'heure.

$\boldsymbol{0,8}$ est la probabilité de passer de l'état "Etre en retard" à "Etre à l'heure",
c'est à dire que Rose soit à l'heure un jour sachant que le jour précedent elle était en retard.

$\boldsymbol{0,7}$ est la probabilité de passer de l'état "Etre à l'heure" à "Etre en retard"
c'est à dire que que Rose soit en retard un jour sachant que le jour précedent elle était à l'heure.

B est l'état qui correspond au fait d'être en retard.

$\boldsymbol{0,3}$ est la probabilité de rester en retard,
c'est à dire que Rose soit en retard un jour
sachant que le jour précedent elle était en retard.

On en déduit:
$\left \{ \begin{array}{l } {\rm P}({\rm A}_{n+1})=a_{n+1}=0,3a_n+0,8b_n \\ {\rm P}({\rm B}_{n+1})=b_{n+1}=0,7a_n+0,2b_n \\ \end{array} \right.$

Pour $\boldsymbol{a_{n+1}}$, on utilise les flèches qui pointent vers A
Pour $\boldsymbol{b_{n+1}}$, on utilise les flèches qui pointent vers B
C'est une autre façon de présenter
la formule des probabilités totales.
Suite $\boldsymbol{\rightarrow}$ Matrice
Il est très important de savoir écrire
un système de suites à l'aide de matrices.

Il y a 2 méthodes:

Avec une matrice colonne:
$\left \{ \begin{array}{l } a_{n+1}=0,3a_n+0,8b_n \\ b_{n+1}=0,7a_n+0,2b_n \\ \end{array} \right.\Leftrightarrow \begin{pmatrix} a_{n+1}\\ b_{n+1} \end{pmatrix}=\begin{pmatrix} 0,3&0,8\\0,7&0,2 \end{pmatrix}\begin{pmatrix} a_{n}\\ b_{n} \end{pmatrix}\Leftrightarrow {\rm X}_{n+1}={\rm A}{\rm X}_n$

avec ${\rm X}_n=\begin{pmatrix} a_{n}\\ b_{n} \end{pmatrix}$
et ${\rm A}=\begin{pmatrix} 0,3&0,8\\0,7&0,2 \end{pmatrix}$

${\rm X}_n$ est une matrice colonne
située à droite de la matrice ${\rm A}$

Avec une matrice ligne:
$\left \{ \begin{array}{l } a_{n+1}=0,3a_n+0,8b_n \\ b_{n+1}=0,7a_n+0,2b_n \\ \end{array} \right.\Leftrightarrow \begin{pmatrix} a_{n+1} & b_{n+1} \end{pmatrix}=\begin{pmatrix} a_{n}& b_{n} \end{pmatrix}\begin{pmatrix} 0,3&0,7\\0,8&0,2 \end{pmatrix}\Leftrightarrow {\rm X}_{n+1}={\rm X}_n{\rm A}$

avec ${\rm X}_n=\begin{pmatrix} a_{n}& b_{n} \end{pmatrix}$
et ${\rm A}=\begin{pmatrix} 0,3&0,7\\0,8&0,2 \end{pmatrix}$

${\rm X}_n$ est une matrice ligne
située à gauche de la matrice ${\rm A}$

L'énoncé souvent impose si ${\rm X}_n$ est une matrice ligne ou colonne.

Attention
ce n'est pas la même matrice A
avec la première et la deuxième méthode!
$\boldsymbol{{\rm X}_{n+1}={\rm A}{\rm X}_n}$

$\boldsymbol{{\rm X}_{n+1}={\rm A}{\rm X}_n}$
1) Démontrer par récurrence que pour tout entier $n\geqslant 0$, $\boldsymbol{{\rm X}_{n}={\rm A}^n{\rm X}_0}$

Il s'agit d'une suite géométrique de matrice.
Et la raison est $\boldsymbol{\rm A}$.

2) Calculer ${\rm A}^n$

Très souvent, vous serez guidé dans l'énoncé.
Il y a 3 méthodes qui sont expliquées sur cette page
$\boldsymbol{{\rm X}_{n+1}={\rm A}{\rm X}_n+{\rm B}}$

$\boldsymbol{{\rm X}_{n+1}={\rm A}{\rm X}_n+{\rm B}}$
1) Chercher une matrice $\boldsymbol{\rm X}$ telle que $\boldsymbol{{\rm X}={\rm A}{\rm X}+B}$

Pour Trouver $\boldsymbol{ \rm X}$:
$\boldsymbol{{\rm X}={\rm A}{\rm X}+B}$
$\boldsymbol{\Leftrightarrow \rm X-AX=B}$

On regroupe les $\boldsymbol{\rm X}$ à gauche
comme avec une équation du type $x=3x+4$.

$\boldsymbol{\Leftrightarrow \rm (I-A)X=B}$

On factorise.
$\boldsymbol{\rm I}$ désigne la matrice identité.

$\boldsymbol{\Leftrightarrow \rm CX=B}$

On appelle $\boldsymbol{\rm C}$ la matrice $\boldsymbol{\rm I-A}$.

$\boldsymbol{\Leftrightarrow \rm C^{-1}CX=C^{-1}B}$

On multiplie par $\boldsymbol{\rm C^{-1}}$ des 2 côtés
sous réserve que $\boldsymbol{\rm C}$ soit inversible.

Pour trouver $\boldsymbol{\rm C^{-1}}$,
on peut utiliser sa calculatrice

$\boldsymbol{\Leftrightarrow \rm X=C^{-1}B}$

Voilà, on a trouvé $\boldsymbol{\rm X}$!

2) On soustrait membre à membre

pour se débarasser de $\boldsymbol{\rm B}$

$\begin{align*} \boldsymbol{{\rm X}_{n+1}}&\boldsymbol{={\rm A}{\rm X}_n+{\rm B}}\\ \boldsymbol{-\phantom{tttttttt} \rm X}&\boldsymbol{\rm =AX+B}\\ \hline{\boldsymbol{{\rm X}_{n+1}-X}}&{\boldsymbol{={\rm A}({\rm X}_n-{\rm X})}}\\ \end{align*}$
3) On Pose $\boldsymbol{{\rm Y_n}={\rm X_n}-{\rm X}}$
4) On obtient: $\boldsymbol{{\rm Y}_{n+1}={\rm A}{\rm Y}_n}$
5) On démontre que $\boldsymbol{{\rm Y}_n={\rm A}^n{\rm Y}_0}$
6) On déduit que $\boldsymbol{{\rm X}_n={\rm Y}_n+{\rm X}={\rm A}^n{\rm Y}_0+{\rm X}}$

Tout est détaillé dans la vidéo

Corrigé en vidéo

Exercices 1:

Matrice et graphe probabiliste

Un automate peut se trouver dans deux états ${\rm A}$ ou ${\rm B}$. À chaque seconde il peut soit rester dans l'état où il se trouve, soit en changer, avec des probabilités données par le graphe probabiliste ci-dessous.

Pour tout entier naturel $n$, on note $a_n$ la probabilité que l'automate se trouve dans l'état ${\rm A}$ après $n$ secondes et $b_n$ la probabilité que l'automate se trouve dans l'état ${\rm B}$ après $n$ secondes.
Au départ, l'automate est dans l'état ${\rm B}$. Gaspard affirme qu'après 4 secondes, l'automate a autant de chances d'être dans l'état $\rm A$ que d'être dans l'état $\rm B$. Cette affirmation est-elle vraie?

Corrigé en vidéo

Exercices 2:

Matrices : suite du type $U_{n+1} =AU_n$

Des souris sont dans une cage comportant deux compartiments A et B. La porte entre ces compartiments est ouverte dix minutes tous les jours. Chaque jour 20% des souris du compartiment A passent dans le compartiment B et 10% des souris qui étaient dans le compartiment B passent dans le compartiment A. Pour tout entier naturel $n$, on note $a_{n}$ et $b_{n}$ les proportions de souris présentes respectivement dans les compartiments A et B après $n$ jours et on convient que $a_0 = b_0 =0,5$ et on note $U_{n}$ la matrice $\begin{pmatrix}a_{n}\\b_{n}\end{pmatrix}$.

Exprimer pour tout entier naturel $n$, $a_{n+1}$ et $b_{n+1}$ en fonction de $a_{n}$ et $b_{n}$.
Déterminer la matrice $A$ telle que pour tout entier naturel $n$, $U_{n+1} = AU_{n}$.
Montrer par récurrence que pour tout entier naturel $n$, $U_{n} = A^nU_{0}$.
On admet que pour tout entier naturel $n$, $A^n = \begin{pmatrix}\frac{1 +2 \times 0,7^n}{3}&\frac{1 - 0,7^n}{3}\\ \frac{2 - 2 \times 0,7^n}{3}&\frac{2 + 0,7^n}{3}\end{pmatrix}$.
Que peut-on dire de la répartition à long terme des souris dans les compartiments A et B ?

Corrigé en vidéo

Exercices 3:

Matrices et suites récurrentes linéaires d'ordre 2

Soit $(u_n)$ la suite définie pour tout entier naturel $n$ par : $u_0 = 0$, $u_1 = 1$ et $u_{n+2} = \frac{3}{2}u_{n+1} - \frac{1}{2}u_n$.
Pour tout entier naturel $n$, on pose : $U_n = \begin{pmatrix} u_{n+1} \\ u_{n}\end{pmatrix}$

Donner $U_0$ et $U_1$.
Déterminer la matrice $A$ telle que pour tout entier naturel $n$, on ait : $U_{n+1} = A U_n$.
Donner sans justifier pour tout entier naturel $n$, $U_n$ en fonction de $A$, $n$ et $U_0$.
On admet que pour tout entier naturel $n$, on a : $A^n = \dfrac{1}{2^n}\begin{pmatrix}2^{n+1}-1&-2^n+1\\2^{n+1}-2&-2^n+2\end{pmatrix}$.
En déduire, pour tout entier naturel $n$, l'expression de $u_n$ en fonction de $n$ puis donner la limite de la suite $(u_n)$.

Corrigé en vidéo

Exercices 4:

Matrices : une suite du type $U_{n+1} = AU_n + B$

Soit $(U_n)$ la suite de matrices de taille $(2~;~1)$ définie pour tout entier naturel $n$ par :
$U_0 = \begin{pmatrix}0\\1\end{pmatrix}$ et $U_{n+1} = AU_n + B$ avec $A = \begin{pmatrix}1/2&1\\0&1/2\end{pmatrix}$ et $B = \begin{pmatrix}1\\1\end{pmatrix}$

Calculer $A(I_2-A)$ et en déduire que la matrice $I_2-A$ est inversible. Donner $(I_2-A)^{-1}$.
Déterminer la matrice $L$ de taille $(2~;~1)$ qui vérifie $L = AL + B$.
Pour tout entier naturel, on pose $V_n = U_n - L$.
1. Montrer que pour tout entier naturel, $V_{n+1} = AV_n$.
2. En déduire une expression de $V_n$ puis de $U_n$ en fonction de $A$ et $n$.
On admet que la suite $(A^n)$ tend vers la matrice nulle d'ordre $2$ lorsque $n$ tend vers l'infini.
Que peut-on en déduire pour la suite $(U_n)$ ?

Corrigé en vidéo

Exercices 5:

Marches aléatoires : le cours à travers un exemple

Dans un pays imaginaire, s'il fait beau et sec un jour, il fera encore beau et sec avec une probabilité de $5/6$ le lendemain. Dans le cas contraire, il fera humide. S'il fait humide un jour, on convient également qu'il fera encore humide avec une probabilité de $2/3$ et qu'il fera beau et sec sinon. Aujourd'hui, il fait beau et sec.
On note:
$A_n$ l'événement : "il fait beau et sec dans $n$ jours"
$B_n$ l'événement : "il fait humide dans $n$ jours".
Calculer ${ \rm P}(A_n) = p_n$ et ${\rm P}(B_n) = q_n$ pour tout entier $n$.

Corrigé en vidéo

Exercices 6:

Marches aléatoires : un problème d'urnes

On dispose de deux urnes U et V contenant chacune deux boules. Au départ, l'urne U contient deux boules blanches et l'urne V contient deux boules noires. On effectue des tirages successifs dans ces urnes de la façon suivante : chaque tirage consiste à prendre au hasard, de manière simultanée, une boule dans chaque urne et à la mettre dans l'autre urne.
Ce processus peut être vue comme une marche aléatoire sur un espace à trois états : $A$ : "il y a 0 boule blanche dans U", $B$ : "il y a 1 boule blanche dans U" et $C$ : "il y a 2 boules blanches dans U".

Représenter la situation à l'aide d'un graphe probabiliste.
Pour tout entier naturel $n$, on note $P_n$ la matrice d'état du système après $n$ tirages. On a donc en particulier $P_0 = \begin{pmatrix}0 & 0& 1\end{pmatrix}$. Déterminer la matrice de transition $T$ telle que pour tout entier naturel $n$, $P_{n+1} = P_nT$.
On admet que la suite de matrices $(P_n)$ converge vers une matrice d'état stable $P$ qui vérifie $P = PT$. Déterminer $P$ et interpréter.

Corrigé en vidéo

Exercices 7:

Marches aléatoires Bac S spé maths Polynésie 2016

Un mobile peut occuper deux positions $\rm A$ et $\rm B$. À chaque étape, il peut soit rester dans la position dans laquelle il se trouve, soit en changer. Pour tout entier naturel $n$, on note :
${\rm A}_n$ l'évènement « le mobile se trouve dans la position A à l'étape $n$ » et $a_n$ sa probabilité.
${\rm B}_n$ l'évènement « le mobile se trouve dans la position B à l'étape $n$ » et $b_n$ sa probabilité.
$\rm{X}_n$ la matrice colonne $\begin{pmatrix} a_n \\ b_n \end{pmatrix}$.
On admet que, pour tout entier naturel $n$, $\rm{X}_{n+1}={\rm M}\times \rm{X}_n$ avec ${\rm M}=\begin{pmatrix} 0,55 ~& 0,3 \\ 0,45 & 0,7 \end{pmatrix}$.

Déterminer la probabilité de ${{\rm P_A}}_n({\rm B}_{n+1})$.
Existe-t-il un état initial $\rm{X}_0 = \begin{pmatrix} a_0 \\ b_0 \end{pmatrix}$ tel que la probabilité d'être en $\rm B$ à l'étape 1 est trois fois plus grande que celle d'être en $\rm A$ à l'étape 1, autrement dit tel que $b_1=3a_1$?

Corrigé en vidéo

Exercices 8:

Marches aléatoires sur un triangle Bac S spé maths Métropole 2015

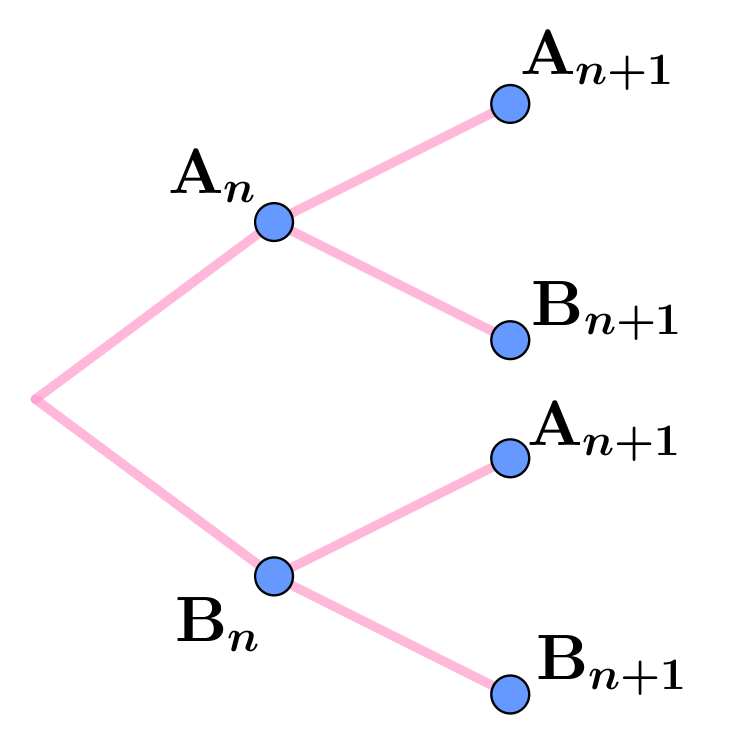
Une boîte contient 3 jetons rouges, 4 verts et 18 blancs. On considère la marche aléatoire d'un pion (au départ en A) sur un triangle ABC. À chaque étape, on tire au hasard un des jetons puis on le remet dans la boîte.
$\bullet~~$Lorsqu'on est en A, si le jeton tiré est rouge, le pion va en B, vert en C, blanc reste en A.
$\bullet~~$Lorsqu'on est en B, si le jeton tiré est rouge, le pion va en A, vert en C, blanc reste en B.
$\bullet~~$Lorsqu'on est en C, si le jeton tiré est rouge, le pion va en A, vert en B, blanc reste en C.
Pour tout entier naturel $n$, on note $a_n$, $b_n$ et $c_n$ les probabilités que le pion soit respectivement sur les sommets A, B et C à l'étape $n$. On note $X_n$ la matrice ligne $\begin{pmatrix}a_n& b_n& c_n\end{pmatrix}$.

Déterminer la matrice $T$ telle que pour tout entier naturel $n$, $X_{n+1} = X_nT$.
On admet que $T = PDP^{-1}$ où $P = \begin{pmatrix}1&7&4\\ 1&-3&4\\1&-3&-7\end{pmatrix}$ et $D = \begin{pmatrix}1&0&0&\\0&0,6&0\\0&0&0,56\end{pmatrix}$.
1. Montrer que pour tout entier naturel $n$, $T^n = PD^nP^{-1}$.
2. Donner sans justification les coefficients de la matrice $D^n$.
On note $\alpha_n,\:\beta_n,\:\gamma_n$ les coefficients de la première ligne de la matrice $T^n$ et on admet que : $\displaystyle \alpha_n = \frac{3}{10} + \frac{7}{10} \times 0,6^n$ et $\displaystyle \beta_n = \frac{37 - 77 \times 0,6^n + 40 \times 0,56^n}{110}$.
On rappelle que, pour tout entier naturel $n$, $X_n = X_0T^n$.
1. Déterminer les nombres $a_n$, $b_n$, à l'aide des coefficients $\alpha_n$ et $\beta_n$. En déduire $c_n$.
2. Déterminer les limites des suites $\left(a_n\right)$, $\left(b_n\right)$ et $\left(c_n\right)$.
3. Sur quel sommet a-t-on le plus de chance de se retrouver après un grand nombre d'étapes ?

Corrigé en vidéo

Exercices 9:

Marches aléatoires : le problème du collectionneur - Problème ouvert

Une marque de corn flakes donne en cadeau une figurine dans chacun de ses paquets. Il y a $3$ figurines différentes. Combien faut-il acheter de paquets pour être sûr à au moins 90% d'avoir la collection complète (en supposant que les différentes figurines sont équitablement réparties dans les paquets) ?

Matrice - Evolution - Graphe

Matrice et évolution

Matrice et graphe probabiliste

Matrices : suite du type $U_{n+1} =AU_n$

Matrices et suites récurrentes linéaires d'ordre 2

Matrices : une suite du type $U_{n+1} = AU_n + B$

Marches aléatoires : le cours à travers un exemple

Marches aléatoires : un problème d'urnes

Marches aléatoires Bac S spé maths Polynésie 2016

Marches aléatoires sur un triangle Bac S spé maths Métropole 2015

Marches aléatoires : le problème du collectionneur - Problème ouvert