Exercice
1: Reconnaitre une
fonction continue -
continuité
en un point
- sur un intervalle
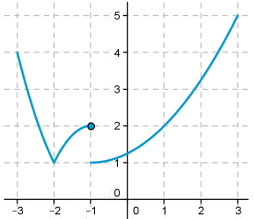
On a tracé la courbe d'une fonction \(f\) définie sur [-3;3].
1) La fonction est-elle continue :
a) en -3 b) en -2 c) en -1
d) en 3?
2) La fonction est-elle continue sur :
a) [-3;1] b) [-3;-2] c) [-3;-1[
d) [-2;-1] e) [-1;3] f) ]-1;3]?
Exercice
2: Reconnaitre une
fonction continue -
continuité
en un point
- sur un intervalle
On considère la fonction \(f\) définie sur \(\mathbb{R}\) par
\[f(x)=\left\{\begin{array}{ll}
-2x & \text{ si } x\lt 2 \\
mx-6 & \text{ si }x\geqslant 2\\
\end{array}\right.\]
Pour quelle valeur de $m$, la fonction \(f\) est-elle continue sur \(\mathbb{R}\)?
Exercice
3:
Continuité en point -
Fonction définie par morceaux
On considère la fonction \(f\) définie sur \(\mathbb{R}\) par
\[f(x)=\left\{\begin{array}{l}
x^2-2x+2 \quad\text{ si } x\le 1 \\
\dfrac 1x \quad\quad\quad\quad\quad\text{ si }x>1\\
\end{array}\right.\]
La fonction \(f\) est-elle continue sur \(\mathbb{R}\)?
Exercice
4:
Continuité en point -
Fonction définie par morceaux
On considère la fonction \(f\) définie sur \(\mathbb{R}\) par
\[f(x)=\left\{\begin{array}{l}
x^2-2x+2 \quad\text{ si } x< -1 \\ 6-x^3 \quad\quad\quad\quad\text{si }x\ge -1\\
\end{array}\right.\]
La fonction \(f\) est-elle continue sur \(\mathbb{R}\)?
Exercice
5: Nombre de solution d'une équation et tableau de variations -
théorème des valeurs intermédiaires
On donne le tableau de variations d'une fonction \(f\) définie sur \(\mathbb{R}\backslash\{ -3
\}\).
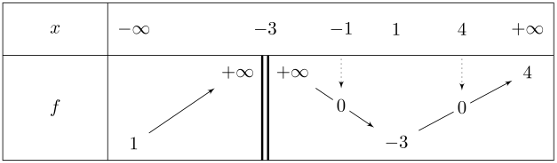
1) Comparer si possible:
a) $f(-5)$ et $f(2)$ b) $f(-5)$ et $f(0)$
c) $f(-2)$ et $f(3)$
2) Dans chaque cas, déterminer le nombre de solutions de l'équation:
a) \(f(x)=-2\) b) \(f(x)=2\)
c) \(f(x)=-4\) d) \(f(x)-5=0\)
3) Déterminer le nombre de solutions de l'équation $f(x)=k$, selon les valeurs de $k$.
4) Déterminer le signe de $f(x)$.
5) Dans chaque cas, déterminer l'image par $f$ de l'intervalle:
a) $]-\infty;-3[$ b) $]-3;+\infty[$
c) $]-3;4[$
6) Déterminer les équations des éventuelles asymptotes horizontales et verticales.
Exercice
6: Justifier qu'une équation a au moins une solution - a une solution
unique - encadrer la solution à 10^-2 près
1) Montrer que l'équation $x^3=2$ admet au moins une solution sur $\mathbb{R}$.
2) Montrer que l'équation $x^3=2$ admet une unique solution sur $\mathbb{R}$, notée $x_0$.
3) Déterminer un encadrement d'amplitude $10^{-1}$ de $x_0$.
Corrigé en vidéo
Exercice
7: Déterminer le nombre de solution d'une équation - Donner un encadrement
- Théorème des valeurs intermédiaires
1) Démontrer que l'équation $x^3-3x=3$ admet au moins une solution dans $\mathbb{R}$.
2) Démontrer que l'équation $x^3-3x=3$ admet une unique solution $\alpha$ dans $\mathbb{R}$.
3) Donner une valeur approchée de $\alpha$ à $10^{-2}$ près.
4) Déterminer le nombre de solutions de l'équation $x^3-3x=k$, selon les valeurs de $k$.
Corrigé en vidéo
Exercice
8: Démontrer qu'une équation admet une solution unique - Donner un
encadrement cette solution
1) Déterminer le nombre de solution de l'équation $3x^4+4x^3=12x^2+1$ dans $\mathbb{R}$.
2) Déterminer un encadrement d'amplitude $10^{-2}$ de chacune des solutions.
Corrigé en vidéo
Exercice
9: Méthode par balayage pour encadrer la solution d'une équation -
Algorithmique
1) Montrer que l'équation $x^3+x-1=0$ admet une unique solution $\alpha$ sur $\mathbb{R}$.
2) Écrire un algorithme pour déterminer par balayage un encadrement d'amplitude $10^{-2}$
de $\alpha$.
Corrigé en vidéo
Exercice
10: Python - Méthode par dichotomie - encadrer la solution d'une équation -
Algorithmique - Python
On considère une fonction $f$ définie, continue, strictement croissante sur un intervalle [a;b] qui s'annule en un réel $\alpha$.
Dans la suite, on prendra comme exemple la fonction $f$ définie sur [2;5] par $f(x)=(x-3)e^x-1$. On admet que cette fonction est bien strictement croissante sur [2;5]
et s'annule en une valeur appelée $\alpha$ sur [2;5].
Écrire une fonction dichotomie en python pour avoir une valeur approchée de $\alpha$ à $10^{-2}$ près.
Corrigé en vidéo
Exercice
11: Méthode par dichotomie pour encadrer racine de 2 -
Algorithmique - Python
Écrire un programme en Python pour déterminer un encadrement de $\sqrt 2$ par dichotomie
d'amplitude
$0,001$.
Corrigé en vidéo
Exercice
12: Méthode par dichotomie pour encadrer la solution d'une équation
Soit $f$ une fonction continue strictement croissante sur $[a;b]$, telle que $f(a)<0$ et
$f(b)>0$.
On sait que l'équation $f(x)=0$ admet une unique solution $\alpha$ sur $[a;b]$.
1) Écrire un algorithme pour déterminer par dichotomie un encadrement d'amplitude $10^{-2}$
de $\alpha$.
2) Application:
a) Justifier que l'équation $x^3+x-1=0$ admet une unique solution $\alpha$ sur
$\mathbb{R}$.
b) Déterminer par dichotomie, un encadrement d'amplitude $10^{-2}$ de
$\alpha$.
3) Généraliser l'algorithme de dichotomie à une fonction strictement monotone.
Exercice
13: Déterminer le nombre de solutions de l'équation f(x)=k selon les valeurs
de k
1) Démontrer que l'équation \[\frac{1}{x-2}=\sqrt{x}\] admet au moins une
solution sur $]2;+\infty[$.
2) Démontrer que l'équation \[\frac{1}{x-2}=\sqrt{x}\] admet une unique
solution $\alpha$ sur $]2;+\infty[$.
3) Déterminer un encadrement de $\alpha$ d'amplitude $10^{-2}$.
Exercice
14: Déterminer le nombre de solutions de l'équation f(x)=k selon les valeurs
de k
L'objectif de cet exercice est de dénombrer le nombre de solutions de l'équation $2x^3+3x^2+1=k$.
On considère la fonction définie sur $\mathbb{R}$ par $f(x)=2x^3+3x^2+1$.
1) Déterminer $f'(x)$ et dresser le tableau de variations de $f$.
2) Déterminer les limites de $f$ en $+\infty$ et $-\infty$.
3) Démontrer que l'équation $2x^3+3x^2+1=0$ admet sur $\mathbb{R}$ une unique solution $\alpha$.
Déterminer un encadrement de $\alpha$ à $10^{-1}$ près.
4) Démontrer que l'équation $2x^3+3x^2=1$ admet exactement 2 solutions sur $\mathbb{R}$.
5) Déterminer le nombre de solutions de l'équation $f(x)=k$, selon les valeurs de $k$.
Corrigé en vidéo
Exercice
15: Etude complète d'une fonction - nombre de solutions de l'équation f(x)=k
selon les valeurs de k
On considère la fonction définie sur $]-\infty;1[\cup ]1;+\infty[$ par $\displaystyle
f(x)=\frac{x^3}{x-1}$.
1) Étudier les variations de $f$.
2) Déterminer les limites aux bornes du domaine de définition.
3) Déterminer le nombre de solutions de l'équation $f(x)=k$, selon les valeurs de $k$.
Exercice
16: Déterminer le nombre de solution d'une équation avec ou sans le théorème
des valeurs intermédiaires
1) Déterminer le nombre de solution de l'équation $x^4+4x^3=1$ sur $\mathbb{R}$.
2) Démontrer que l'équation $x^4+4x^3=0$ admet 2 solutions sur $\mathbb{R}$:
a) A l'aide du théorème des valeurs intermédiaires.
b) Sans utiliser le théorème des valeurs intermédiaires.
3) Peut-on appliquer la méthode du 2)b) à la question 1)? Justifier.
Exercice
17: Déterminer le nombre de solutions de l'équation f(x)=k selon les
valeurs de k
On considère la fonction définie sur $\mathbb{R}$ par $f(x)=x^3-2x^2+1$.
1) Étudier les variations de $f$.
2) Déterminer le nombre de solutions de l'équation $f(x)=k$, selon les valeurs de $k$.
Corrigé en vidéo
Exercice
18: Etude des variations à l'aide fonction auxiliaire et théorème des
valeurs intermédaires
On considère la fonction $f$ définie sur $\mathbb{R}\backslash\{ -1 \}$ par
\[f(x)=\frac{x^2+1}{x^3+1}\].
1) Pour tout réel $x\ne-1$, déterminer $f'(x)$.
2) On considère la fonction $P$ définie sur $\mathbb{R}$ par $P(x)=-x^3-3x+2$.
a) Étudier les variations de $P$ sur $\mathbb{R}$.
b) En déduire que l'équation $P(x)=0$ admet une unique solution notée $\alpha$
sur $\mathbb{R}$.
c) En déduire le signe de $P(x)$ sur $\mathbb{R}$.
d) Démontrer que $0.5
< \alpha < 0.6$
e) Démontrer que
\[f(\alpha)=\frac 2{3\alpha}\].
En déduire un encadrement de $f(\alpha)$.
Pour montrer que \[f(\alpha)=\frac 2{3\alpha}\] :
utiliser la définition de $\alpha$.
3) En déduire le signe de $f'(x)$ et les variations de $f$ sur $\mathbb{R}\backslash\{ -1 \}$.
Penser à exprimer $f'(x)$ à l'aide de $P(x)$.
Exercice
19: solution de l'équation x+x²+...x^n=1 - Théorème des valeurs
intermédiaires
Soit un entier $n \ge 2$.
On considère la fonction définie sur $[0;1]$ par $f_n(x)=x+x^2+...+x^n$
1) Démontrer que l'équation $x+x^2+...+x^n=1$ admet une unique
solution sur [0;1]. On note $a_n$ cette solution.
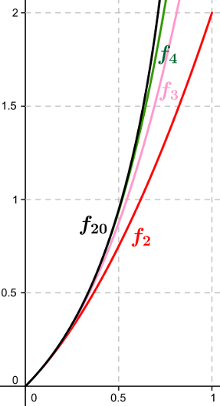
2) On a tracé les courbes des fonctions $f_2$, $f_3$, $f_4$, $f_{20}$.
Déterminer graphiquement une valeur approchée de $a_2$, $a_3$, $a_4$,
$a_{20}$.
Conjecturer le sens de variation de $(a_n)$ et sa limite.
3) Déterminer la valeur exacte de $a_2$.
4) Pour $x\in [0;1]$, comparer $f_n(x)$ et $f_{n+1}(x)$.
5) Démontrer que pour $n\ge 2$, $f_{n+1}(a_n) \ge 1$.
En déduire le sens de variation de $(a_n)$.
6) Justifier que pour $n\ge 2$, \[0\le a_n \le \frac 34\].
7) En déduire que la suite $(a_n)$ converge. On note $\ell$ sa limite.
8) En déduire que \[\lim_{\substack{n \to +\infty}}f_n(a_n)=\frac
1{1-\ell}-1\].
En déduire la valeur de $\ell$.
Exercice
20: Problème ouvert - solution de l'équation
f(x)=x - Théorème
des valeurs intermédiaires
Soit $f$ une fonction définie et continue sur [0;1] telle que pour tout $x$ de [0;1], $0\le f(x)\le
1$.
Montrer qu'il existe au moins un nombre $a$ de [0;1] tel que $f(a)=a$.
Corrigé en vidéo!
Exercice
21:Théorème des valeurs intermédiaires: Problème ouvert - fonction
trigonométrique
Déterminer le nombre de solutions dans $\mathbb{R}$ de l'équation (E) $\cos x=x$.
Donner un encadrement de chacune de ces solutions à 0,01 près.
Exercice
22: Problème ouvert
Dénombrer les solutions dans $\mathbb{R}$ de l'équation (E) $\sin x=x^2$.
Web
