
























































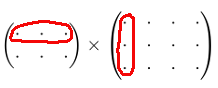


$\begin{pmatrix} \cdot & 5\\ \cdot & 3\\ \cdot & 2 \end{pmatrix}$

Ici on écrit la matrice B
| |
$\begin{pmatrix} \cdot & \cdot & \cdot \\ \cdot & \cdot & \cdot\\2&1&3\\\cdot & \cdot & \cdot\end{pmatrix}$

Ici on place la matrice A
|
$\begin{pmatrix}\cdot & \cdot \\ \cdot & \cdot\\ \cdot & 19 \\ \cdot & \cdot\end{pmatrix}$

Ici on otient $\rm A\times B$
$19=2\times 5+1\times 3+3\times 2$ |









 Savoir utiliser sa calculatrice CASIO avec les matrices
Savoir utiliser sa calculatrice CASIO avec les matrices







|
|



















N'hesitez pas à envoyer un mail à:
jaicompris.com@gmail.com